Full infer Pipeline Examples

Introduction

This vignette is intended to provide a set of examples that nearly exhaustively demonstrate the functionalities provided by infer. Commentary on these examples is limited—for more discussion of the intuition behind the package, see the “Getting to Know infer” vignette, accessible by calling vignette("infer").

Throughout this vignette, we’ll make use of the gss dataset supplied by infer, which contains a sample of data from the General Social Survey. See ?gss for more information on the variables included and their source. Note that this data (and our examples on it) are for demonstration purposes only, and will not necessarily provide accurate estimates unless weighted properly. For these examples, let’s suppose that this dataset is a representative sample of a population we want to learn about: American adults. The data looks like this:

# load in the dataset
data(gss)

# take a look at its structure
dplyr::glimpse(gss)

## Rows: 500
## Columns: 11
## $ year    <dbl> 2014, 1994, 1998, 1996, 1994, 1996, 1990, 2016, 2000, 19…
## $ age     <dbl> 36, 34, 24, 42, 31, 32, 48, 36, 30, 33, 21, 30, 38, 49, …
## $ sex     <fct> male, female, male, male, male, female, female, female, …
## $ college <fct> degree, no degree, degree, no degree, degree, no degree,…
## $ partyid <fct> ind, rep, ind, ind, rep, rep, dem, ind, rep, dem, dem, i…
## $ hompop  <dbl> 3, 4, 1, 4, 2, 4, 2, 1, 5, 2, 4, 3, 4, 4, 2, 2, 3, 2, 1,…
## $ hours   <dbl> 50, 31, 40, 40, 40, 53, 32, 20, 40, 40, 23, 52, 38, 72, …
## $ income  <ord> $25000 or more, $20000 - 24999, $25000 or more, $25000 o…
## $ class   <fct> middle class, working class, working class, working clas…
## $ finrela <fct> below average, below average, below average, above avera…
## $ weight  <dbl> 0.8960, 1.0825, 0.5501, 1.0864, 1.0825, 1.0864, 1.0627, …

Hypothesis tests

One numerical variable (mean)

Calculating the observed statistic,

x_bar <- gss %>%
  specify(response = hours) %>%
  calculate(stat = "mean")

Alternatively, using the observe() wrapper to calculate the observed statistic,

x_bar <- gss %>%
  observe(response = hours, stat = "mean")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(response = hours) %>%
  hypothesize(null = "point", mu = 40) %>%
  generate(reps = 1000) %>%
  calculate(stat = "mean")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = x_bar, direction = "two-sided")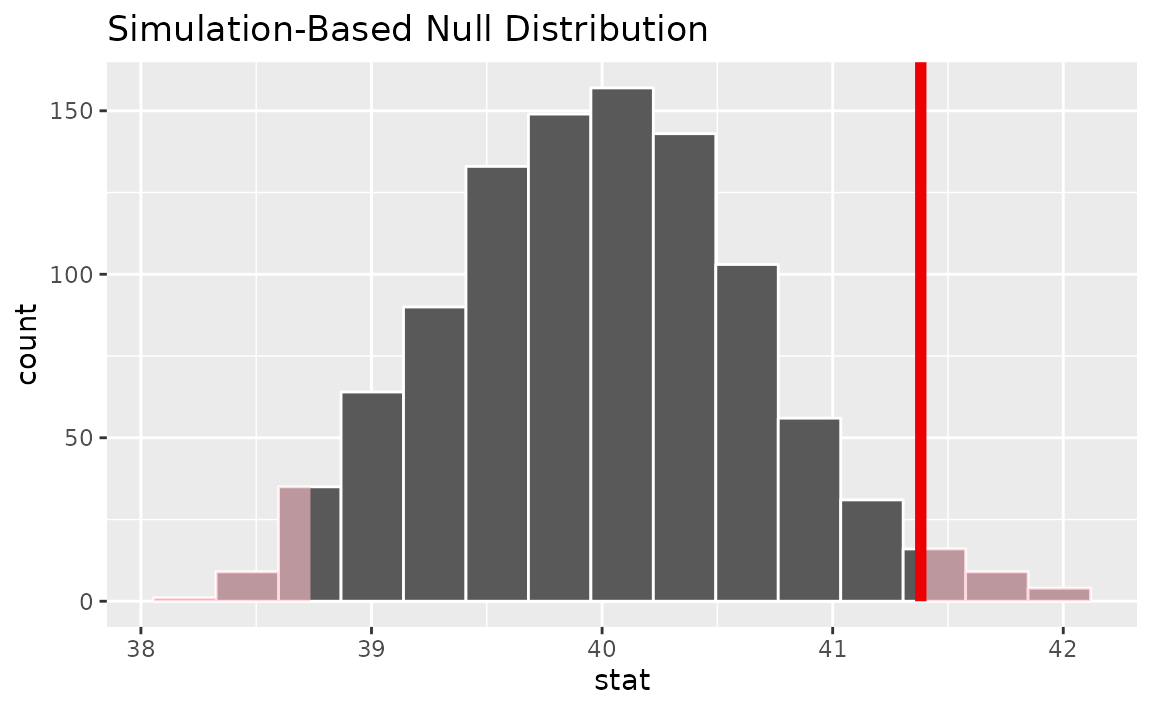

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = x_bar, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.048

One numerical variable (standardized mean \(t\))

Calculating the observed statistic,

t_bar <- gss %>%
  specify(response = hours) %>%
  hypothesize(null = "point", mu = 40) %>%
  calculate(stat = "t")

Alternatively, using the observe() wrapper to calculate the observed statistic,

t_bar <- gss %>%
  observe(response = hours, null = "point", mu = 40, stat = "t")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(response = hours) %>%
  hypothesize(null = "point", mu = 40) %>%
  generate(reps = 1000) %>%
  calculate(stat = "t")

Alternatively, finding the null distribution using theoretical methods using the assume() verb,

null_dist_theory <- gss %>%
  specify(response = hours)  %>%
  assume("t")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = t_bar, direction = "two-sided")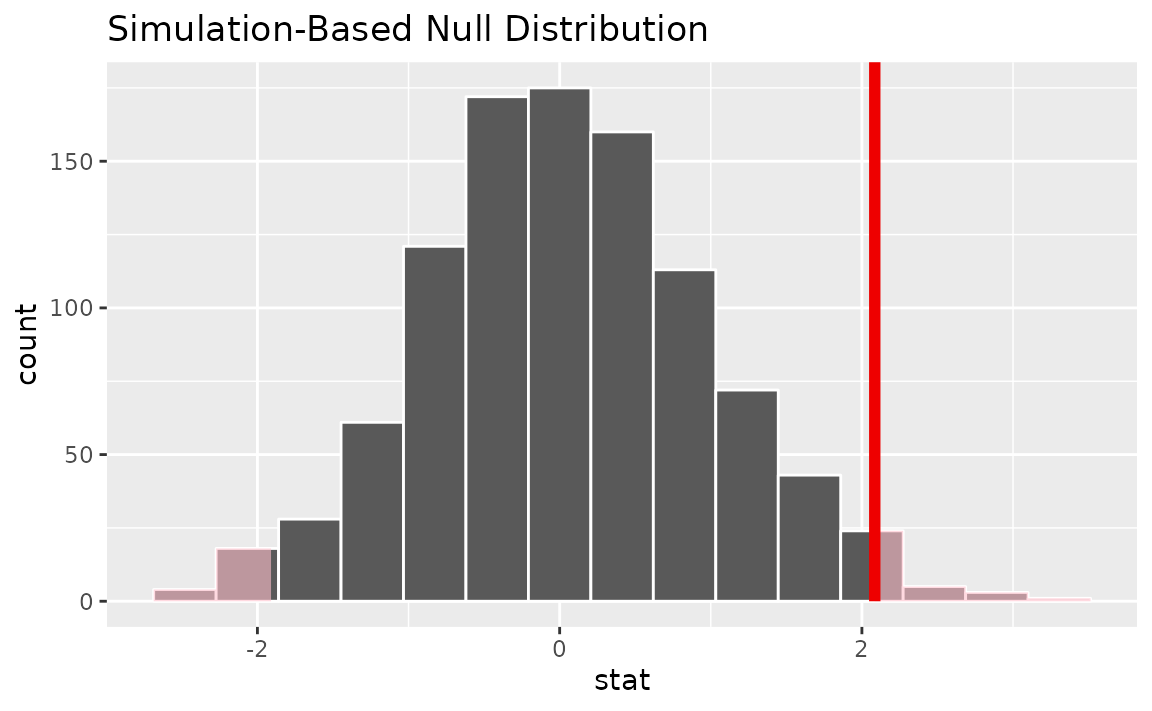

Alternatively, visualizing the observed statistic using the theory-based null distribution,

visualize(null_dist_theory) +
  shade_p_value(obs_stat = t_bar, direction = "two-sided")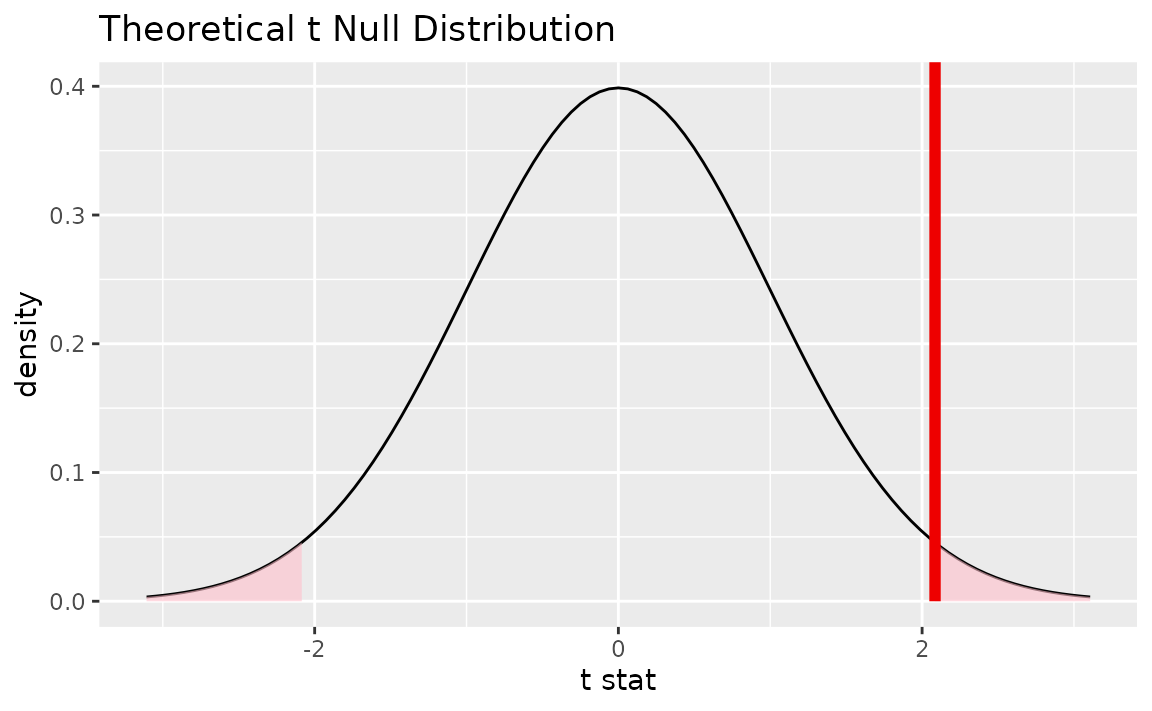

Alternatively, visualizing the observed statistic using both of the null distributions,

visualize(null_dist, method = "both") +
  shade_p_value(obs_stat = t_bar, direction = "two-sided")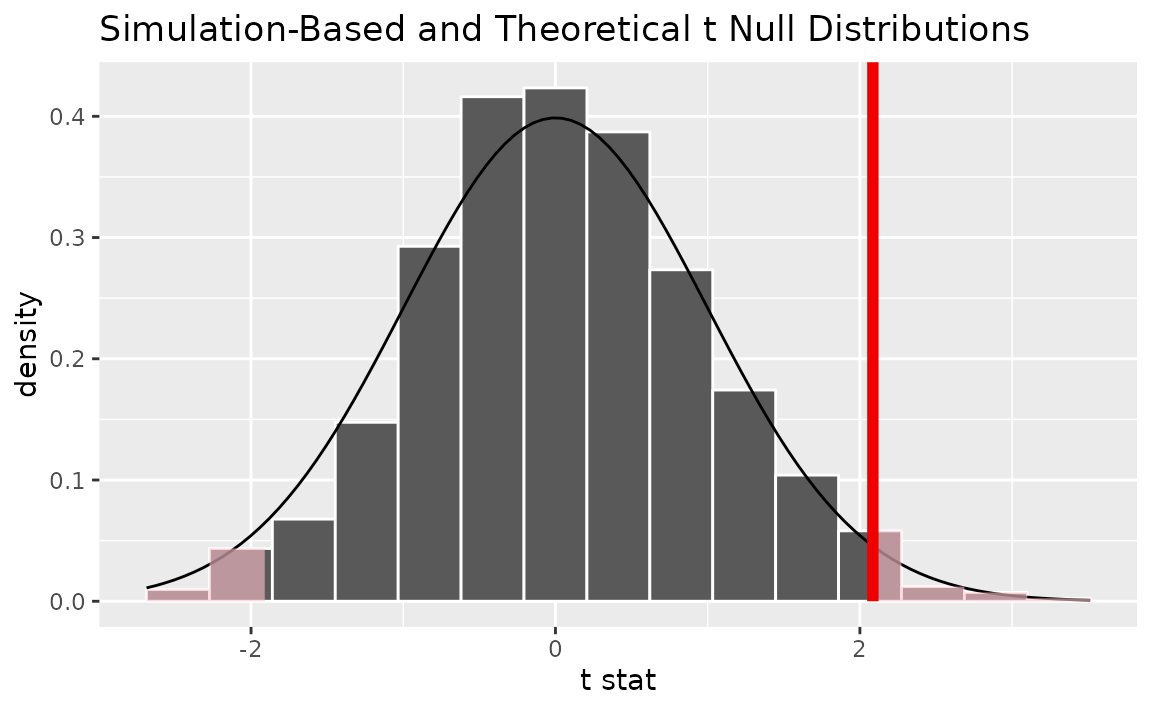

Note that the above code makes use of the randomization-based null distribution.

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = t_bar, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.032

Alternatively, using the t_test wrapper:

gss %>%
  t_test(response = hours, mu = 40)

## # A tibble: 1 × 7
##   statistic  t_df p_value alternative estimate lower_ci upper_ci
##       <dbl> <dbl>   <dbl> <chr>          <dbl>    <dbl>    <dbl>
## 1      2.09   499  0.0376 two.sided       41.4     40.1     42.7

infer does not support testing on one numerical variable via the z distribution.

One numerical variable (median)

Calculating the observed statistic,

x_tilde <- gss %>%
  specify(response = age) %>%
  calculate(stat = "median")

Alternatively, using the observe() wrapper to calculate the observed statistic,

x_tilde <- gss %>%
  observe(response = age, stat = "median")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(response = age) %>%
  hypothesize(null = "point", med = 40) %>% 
  generate(reps = 1000) %>% 
  calculate(stat = "median")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = x_tilde, direction = "two-sided")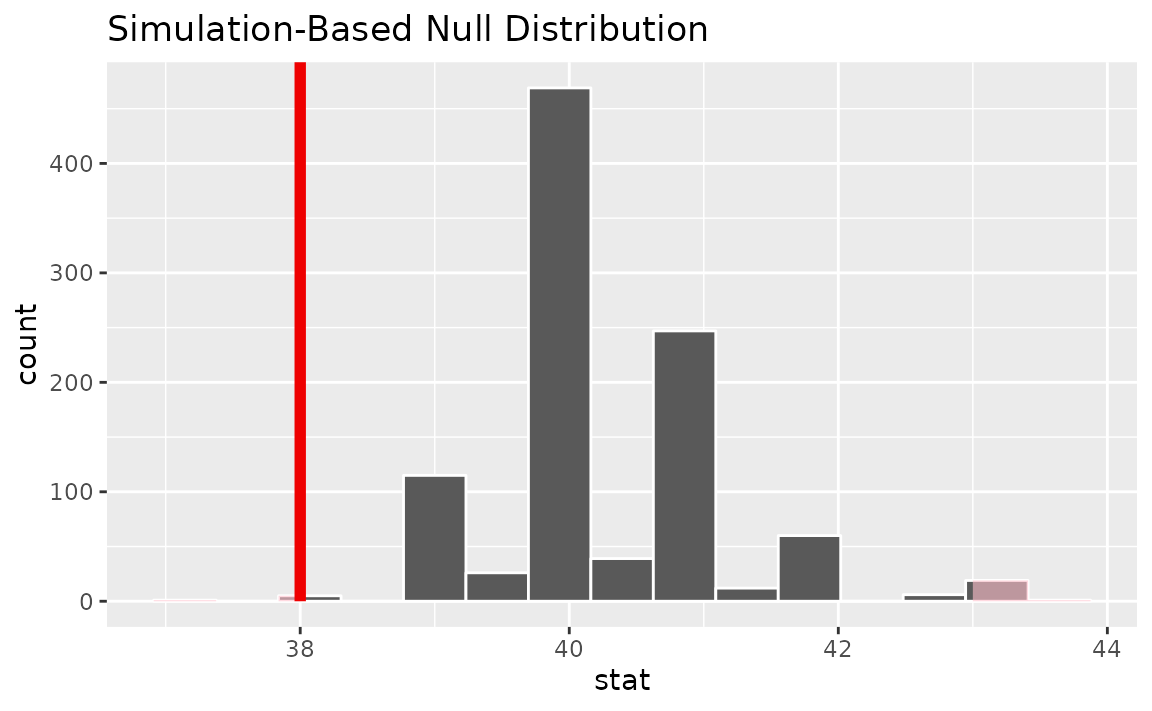

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = x_tilde, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.012

One numerical variable (paired)

The example under this header is compatible with stats "mean", "median", "sum", and "sd".

Suppose that each of these survey respondents had provided the number of hours worked per week when surveyed 5 years prior, encoded as hours_previous.

set.seed(1)

gss_paired <- gss %>%
   mutate(
      hours_previous = hours + 5 - rpois(nrow(.), 4.8),
      diff = hours - hours_previous
   )

gss_paired %>%
   select(hours, hours_previous, diff)

## # A tibble: 500 × 3
##    hours hours_previous  diff
##    <dbl>          <dbl> <dbl>
##  1    50             52    -2
##  2    31             32    -1
##  3    40             40     0
##  4    40             37     3
##  5    40             42    -2
##  6    53             50     3
##  7    32             28     4
##  8    20             19     1
##  9    40             40     0
## 10    40             43    -3
## # ℹ 490 more rows

We’d like to test the null hypothesis that the "mean" hours worked per week did not change between the sampled time and five years prior.

infer supports paired hypothesis testing via the null = "paired independence" argument to hypothesize().

Calculating the observed statistic,

x_tilde <- gss_paired %>%
  specify(response = diff) %>%
  calculate(stat = "mean")

Alternatively, using the observe() wrapper to calculate the observed statistic,

x_tilde <- gss_paired %>%
  observe(response = diff, stat = "mean")

Then, generating the null distribution,

null_dist <- gss_paired %>%
  specify(response = diff) %>%
  hypothesize(null = "paired independence") %>% 
  generate(reps = 1000, type = "permute") %>% 
  calculate(stat = "mean")

Note that the diff column itself is not permuted, but rather the signs of the values in the column.

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = x_tilde, direction = "two-sided")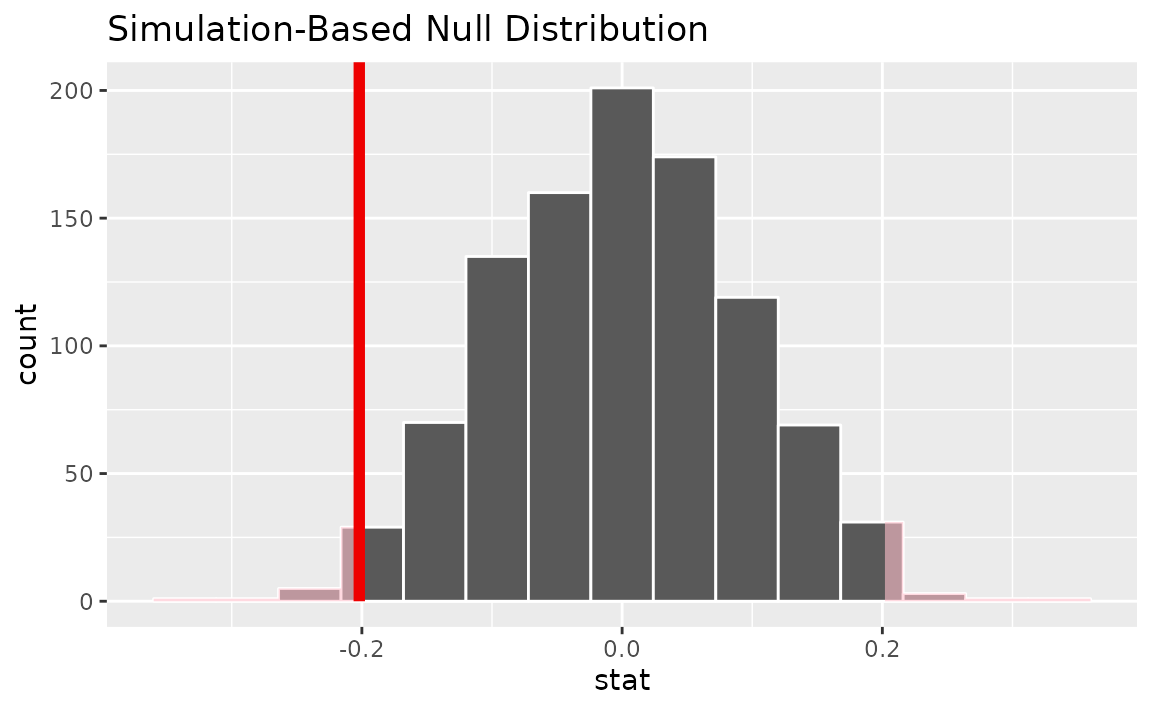

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = x_tilde, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.028

One categorical (one proportion)

Calculating the observed statistic,

p_hat <- gss %>%
  specify(response = sex, success = "female") %>%
  calculate(stat = "prop")

Alternatively, using the observe() wrapper to calculate the observed statistic,

p_hat <- gss %>%
  observe(response = sex, success = "female", stat = "prop")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(response = sex, success = "female") %>%
  hypothesize(null = "point", p = .5) %>%
  generate(reps = 1000) %>%
  calculate(stat = "prop")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = p_hat, direction = "two-sided")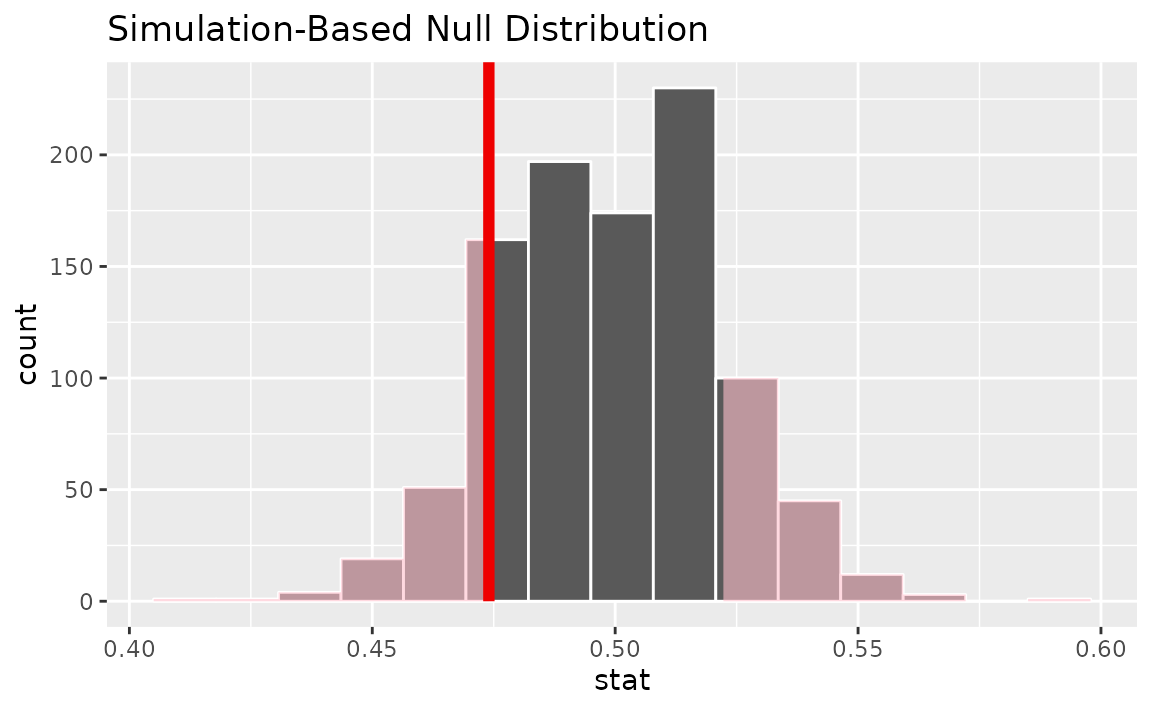

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = p_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.276

Note that logical variables will be coerced to factors:

null_dist <- gss %>%
  dplyr::mutate(is_female = (sex == "female")) %>%
  specify(response = is_female, success = "TRUE") %>%
  hypothesize(null = "point", p = .5) %>%
  generate(reps = 1000) %>%
  calculate(stat = "prop")

One categorical variable (standardized proportion \(z\))

Calculating the observed statistic,

p_hat <- gss %>%
  specify(response = sex, success = "female") %>%
  hypothesize(null = "point", p = .5) %>%
  calculate(stat = "z")

Alternatively, using the observe() wrapper to calculate the observed statistic,

p_hat <- gss %>%
  observe(response = sex, success = "female", null = "point", p = .5, stat = "z")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(response = sex, success = "female") %>%
  hypothesize(null = "point", p = .5) %>%
  generate(reps = 1000, type = "draw") %>%
  calculate(stat = "z")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = p_hat, direction = "two-sided")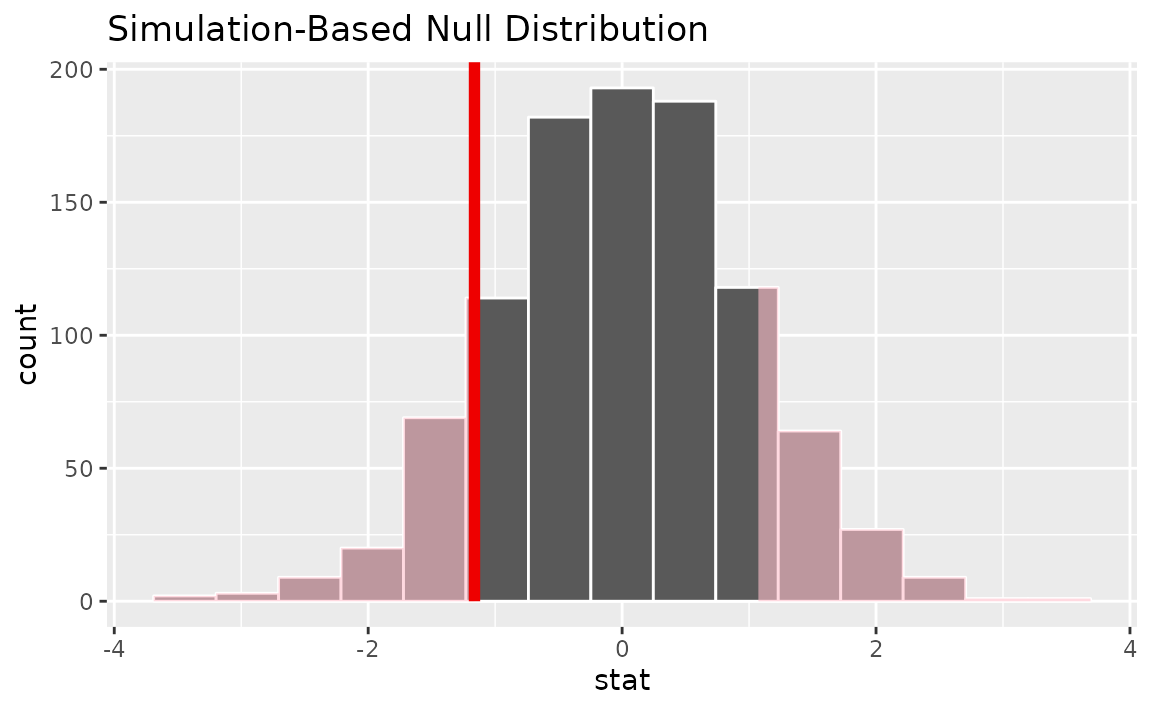

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = p_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.252

The package also supplies a wrapper around prop.test for tests of a single proportion on tidy data.

prop_test(gss,
          college ~ NULL,
          p = .2)

## # A tibble: 1 × 4
##   statistic chisq_df   p_value alternative
##       <dbl>    <int>     <dbl> <chr>      
## 1      636.        1 2.98e-140 two.sided

infer does not support testing two means via the z distribution.

Two categorical (2 level) variables

The infer package provides several statistics to work with data of this type. One of them is the statistic for difference in proportions.

Calculating the observed statistic,

d_hat <- gss %>% 
  specify(college ~ sex, success = "no degree") %>%
  calculate(stat = "diff in props", order = c("female", "male"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

d_hat <- gss %>% 
  observe(college ~ sex, success = "no degree", 
          stat = "diff in props", order = c("female", "male"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(college ~ sex, success = "no degree") %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000) %>% 
  calculate(stat = "diff in props", order = c("female", "male"))

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = d_hat, direction = "two-sided")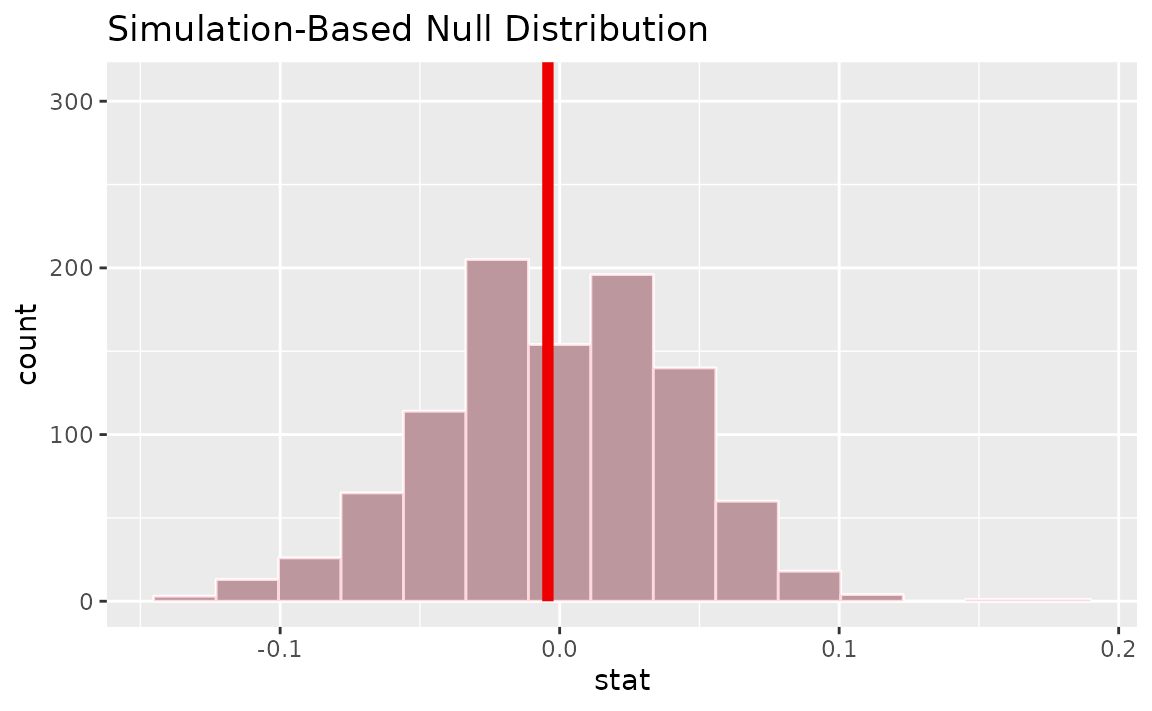

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = d_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1       1

infer also provides functionality to calculate ratios of proportions. The workflow looks similar to that for diff in props.

Calculating the observed statistic,

r_hat <- gss %>% 
  specify(college ~ sex, success = "no degree") %>%
  calculate(stat = "ratio of props", order = c("female", "male"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

r_hat <- gss %>% 
  observe(college ~ sex, success = "no degree",
          stat = "ratio of props", order = c("female", "male"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(college ~ sex, success = "no degree") %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000) %>% 
  calculate(stat = "ratio of props", order = c("female", "male"))

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = r_hat, direction = "two-sided")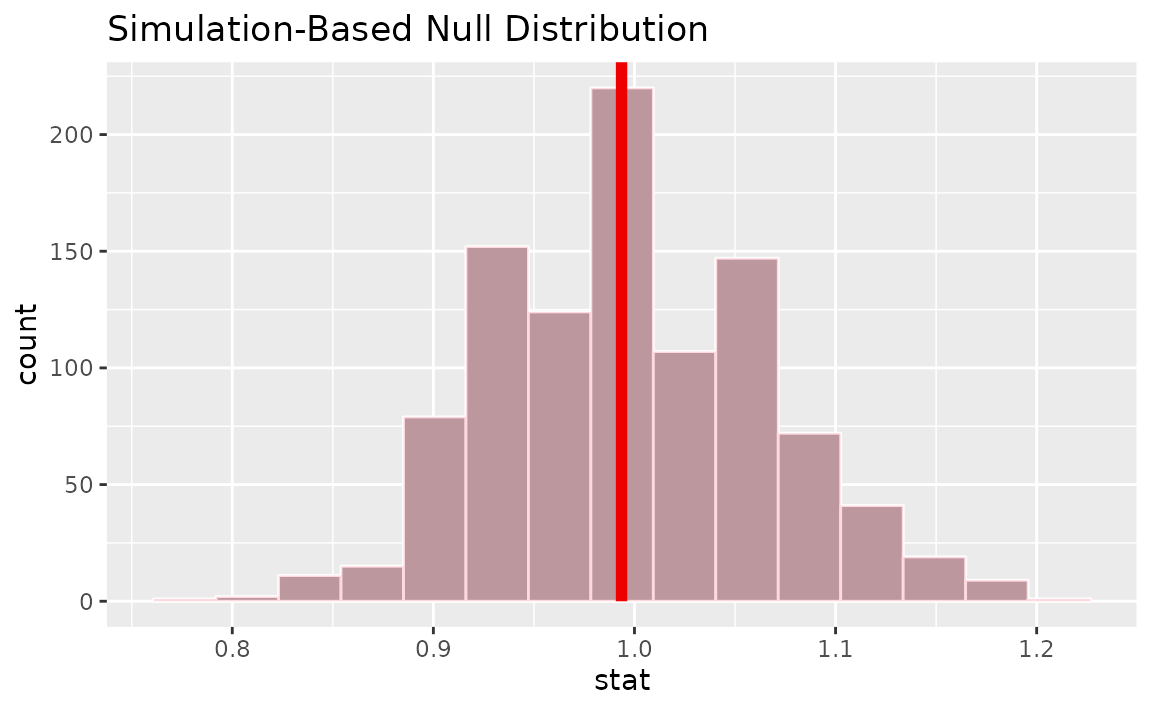

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = r_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1       1

In addition, the package provides functionality to calculate odds ratios. The workflow also looks similar to that for diff in props.

Calculating the observed statistic,

or_hat <- gss %>% 
  specify(college ~ sex, success = "no degree") %>%
  calculate(stat = "odds ratio", order = c("female", "male"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(college ~ sex, success = "no degree") %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000) %>% 
  calculate(stat = "odds ratio", order = c("female", "male"))

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = or_hat, direction = "two-sided")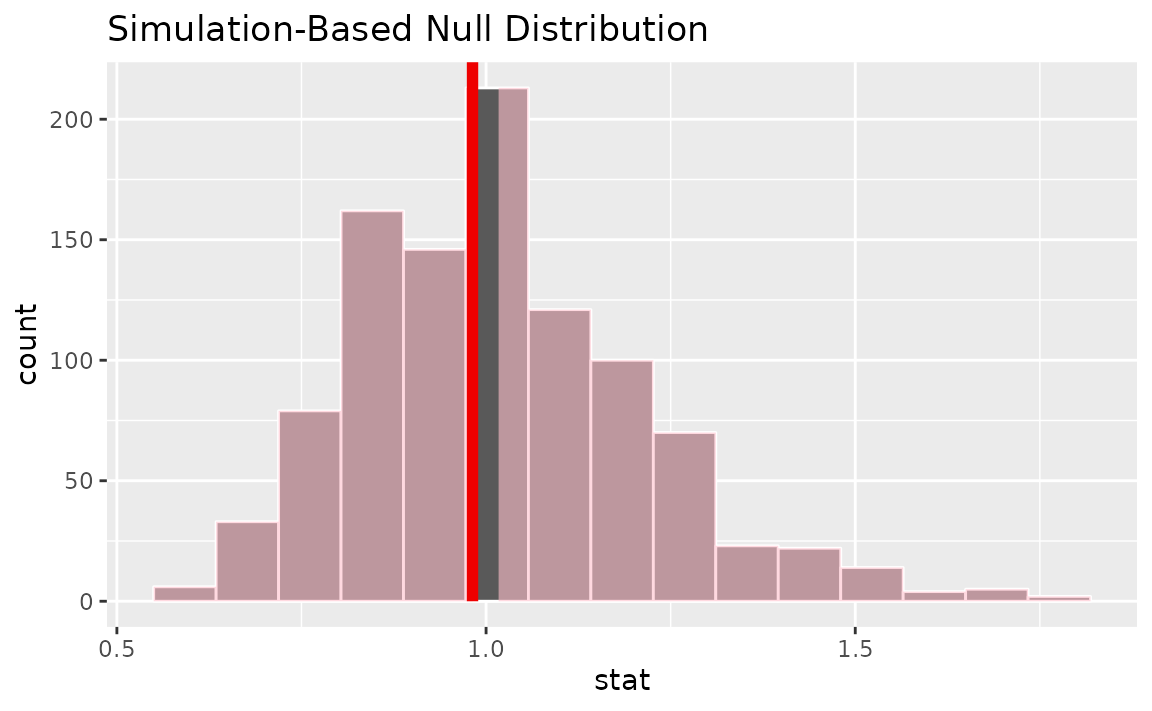

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = or_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.984

Two categorical (2 level) variables (z)

Finding the standardized observed statistic,

z_hat <- gss %>% 
  specify(college ~ sex, success = "no degree") %>%
  hypothesize(null = "independence") %>%
  calculate(stat = "z", order = c("female", "male"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

z_hat <- gss %>% 
  observe(college ~ sex, success = "no degree",
          stat = "z", order = c("female", "male"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(college ~ sex, success = "no degree") %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000) %>% 
  calculate(stat = "z", order = c("female", "male"))

Alternatively, finding the null distribution using theoretical methods using the assume() verb,

null_dist_theory <- gss %>%
  specify(college ~ sex, success = "no degree") %>%
  assume("z")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = z_hat, direction = "two-sided")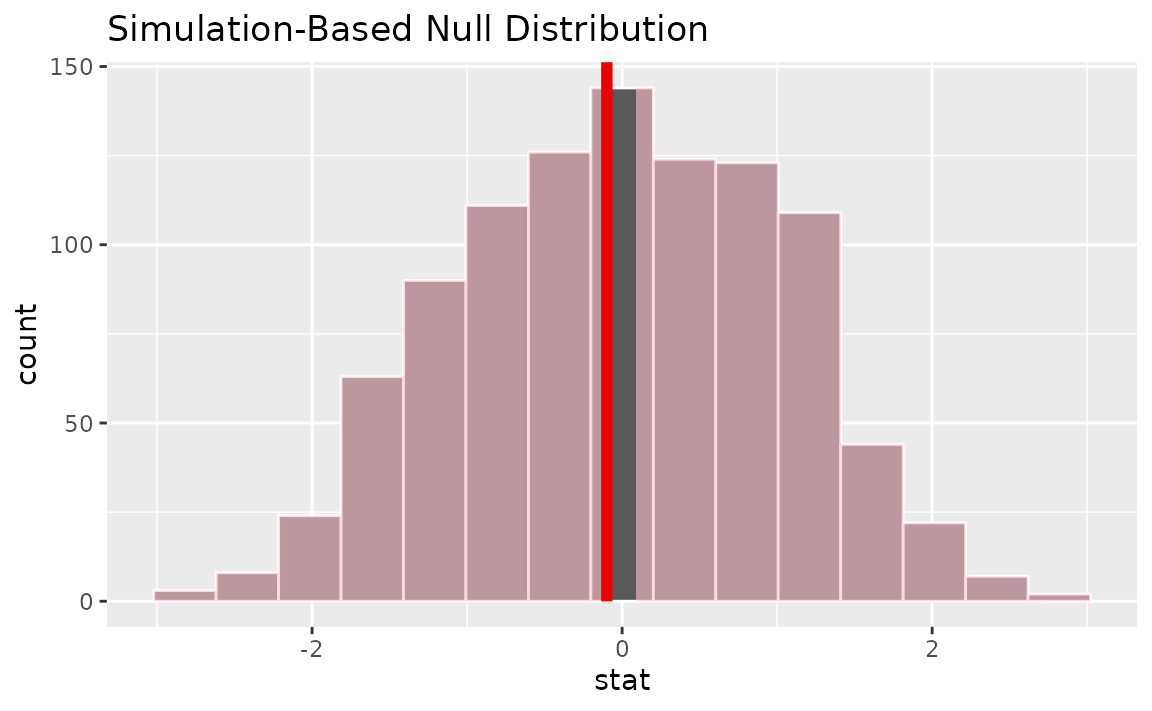

Alternatively, visualizing the observed statistic using the theory-based null distribution,

visualize(null_dist_theory) +
  shade_p_value(obs_stat = z_hat, direction = "two-sided")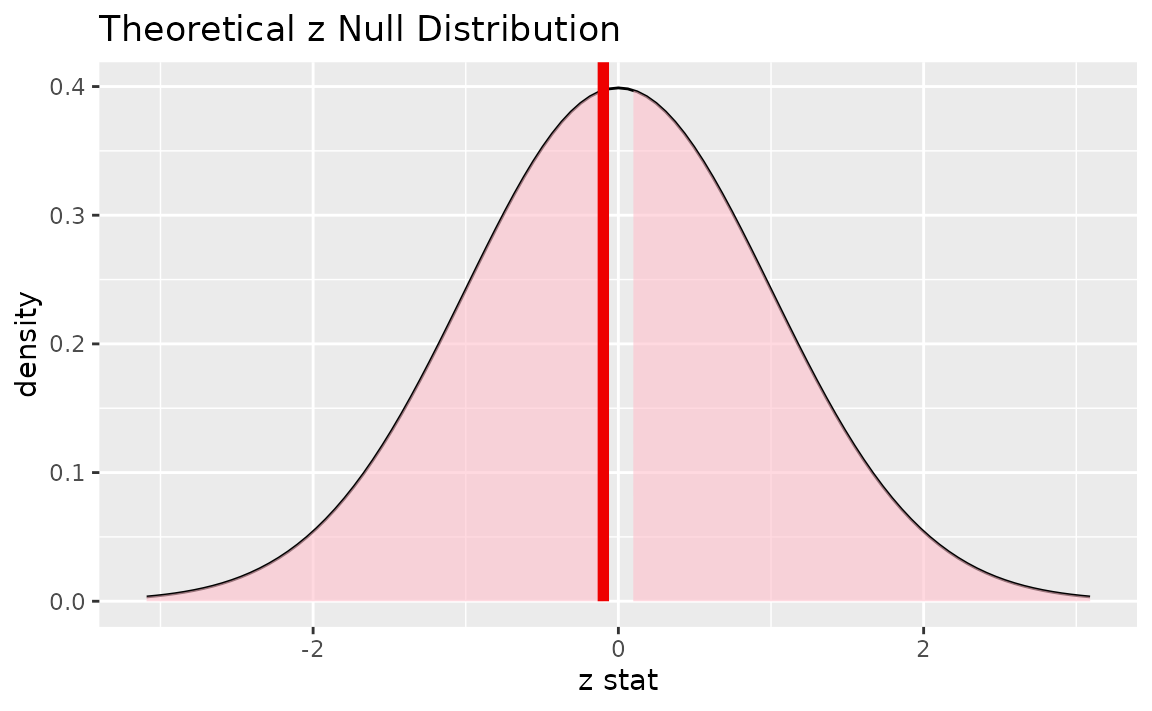

Alternatively, visualizing the observed statistic using both of the null distributions,

visualize(null_dist, method = "both") +
  shade_p_value(obs_stat = z_hat, direction = "two-sided")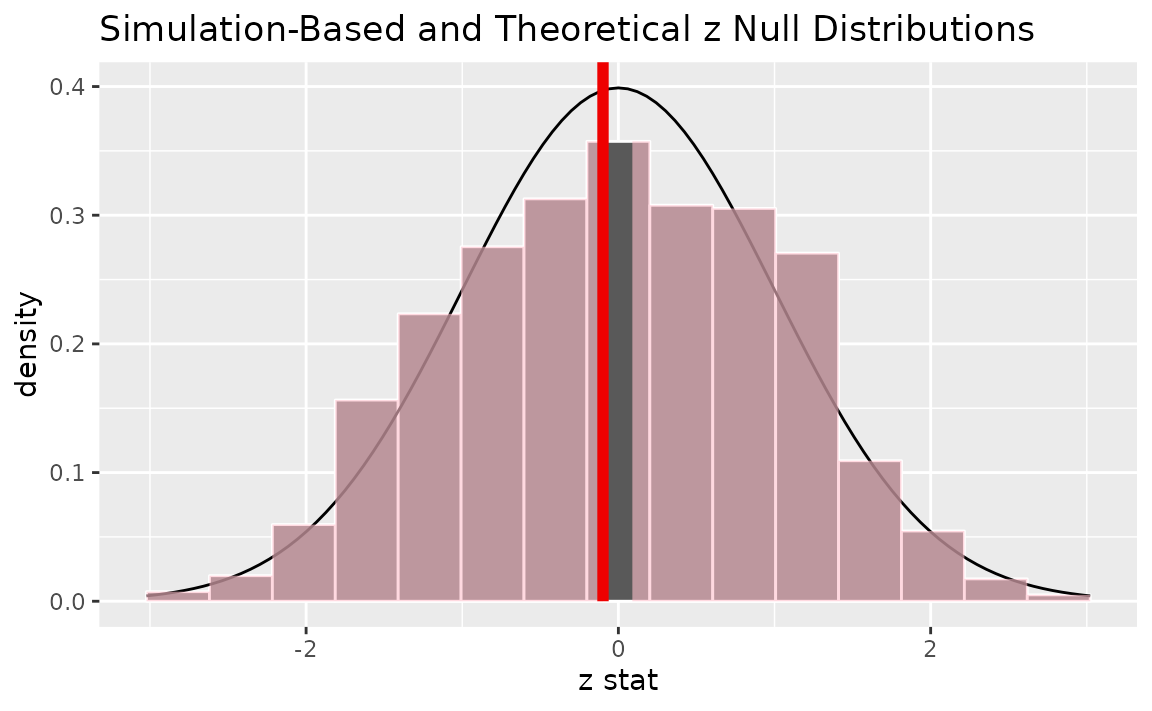

Note that the above code makes use of the randomization-based null distribution.

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = z_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1    0.98

Note the similarities in this plot and the previous one.

The package also supplies a wrapper around prop.test to allow for tests of equality of proportions on tidy data.

prop_test(gss, 
          college ~ sex,  
          order = c("female", "male"))

## # A tibble: 1 × 6
##   statistic chisq_df p_value alternative lower_ci upper_ci
##       <dbl>    <dbl>   <dbl> <chr>          <dbl>    <dbl>
## 1 0.0000204        1   0.996 two.sided    -0.0918   0.0834

One categorical (>2 level) - GoF

Calculating the observed statistic,

Note the need to add in the hypothesized values here to compute the observed statistic.

Chisq_hat <- gss %>%
  specify(response = finrela) %>%
  hypothesize(null = "point",
              p = c("far below average" = 1/6,
                    "below average" = 1/6,
                    "average" = 1/6,
                    "above average" = 1/6,
                    "far above average" = 1/6,
                    "DK" = 1/6)) %>%
  calculate(stat = "Chisq")

Alternatively, using the observe() wrapper to calculate the observed statistic,

Chisq_hat <- gss %>%
  observe(response = finrela,
          null = "point",
          p = c("far below average" = 1/6,
                "below average" = 1/6,
                "average" = 1/6,
                "above average" = 1/6,
                "far above average" = 1/6,
                "DK" = 1/6),
          stat = "Chisq")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(response = finrela) %>%
  hypothesize(null = "point",
              p = c("far below average" = 1/6,
                    "below average" = 1/6,
                    "average" = 1/6,
                    "above average" = 1/6,
                    "far above average" = 1/6,
                    "DK" = 1/6)) %>%
  generate(reps = 1000, type = "draw") %>%
  calculate(stat = "Chisq")

Alternatively, finding the null distribution using theoretical methods using the assume() verb,

null_dist_theory <- gss %>%
  specify(response = finrela) %>%
  assume("Chisq")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = Chisq_hat, direction = "greater")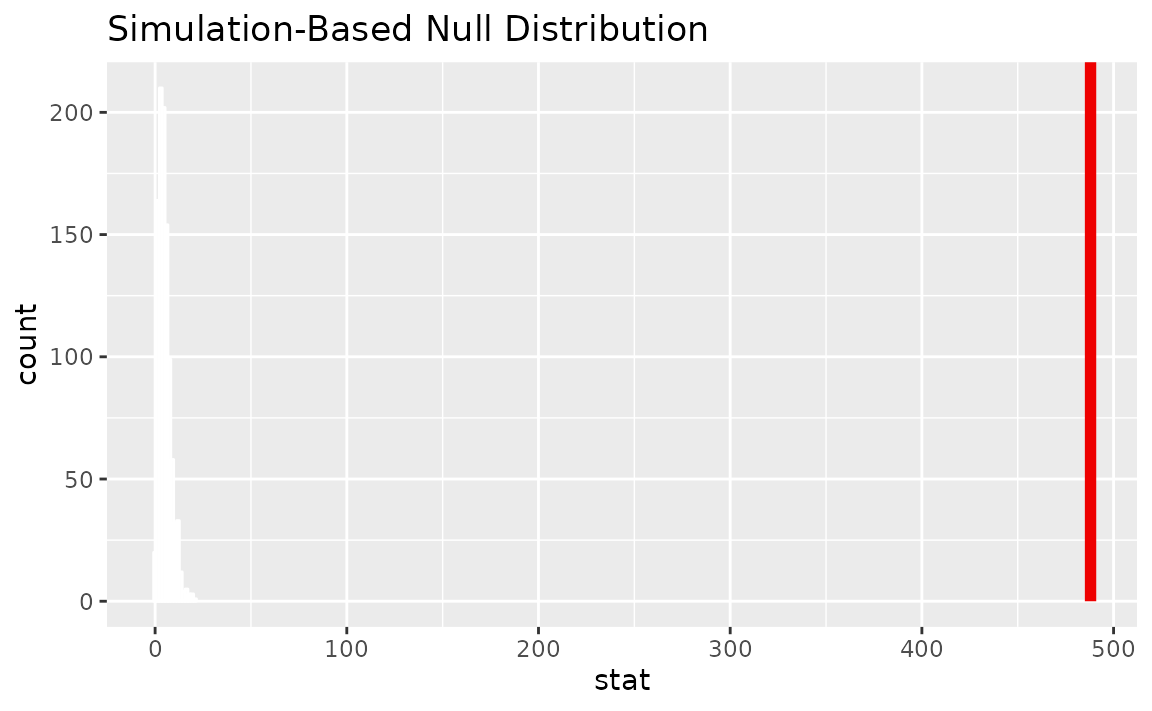

Alternatively, visualizing the observed statistic using the theory-based null distribution,

visualize(null_dist_theory) +
  shade_p_value(obs_stat = Chisq_hat, direction = "greater")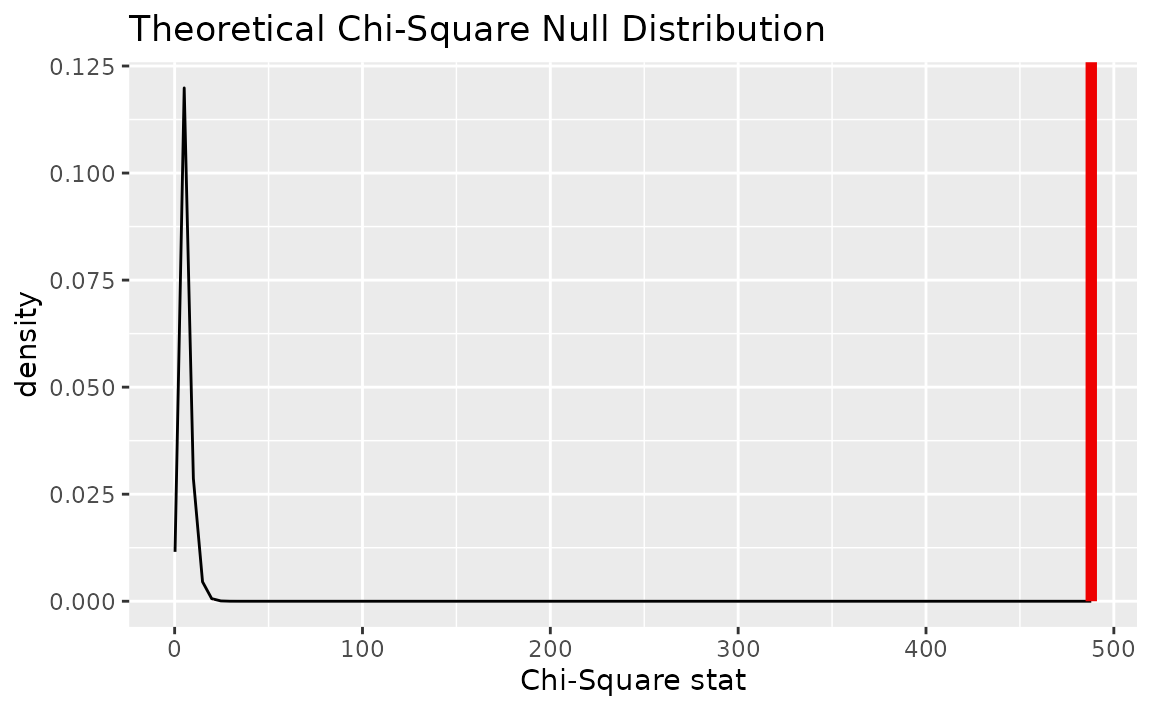

Alternatively, visualizing the observed statistic using both of the null distributions,

visualize(null_dist_theory, method = "both") +
  shade_p_value(obs_stat = Chisq_hat, direction = "greater")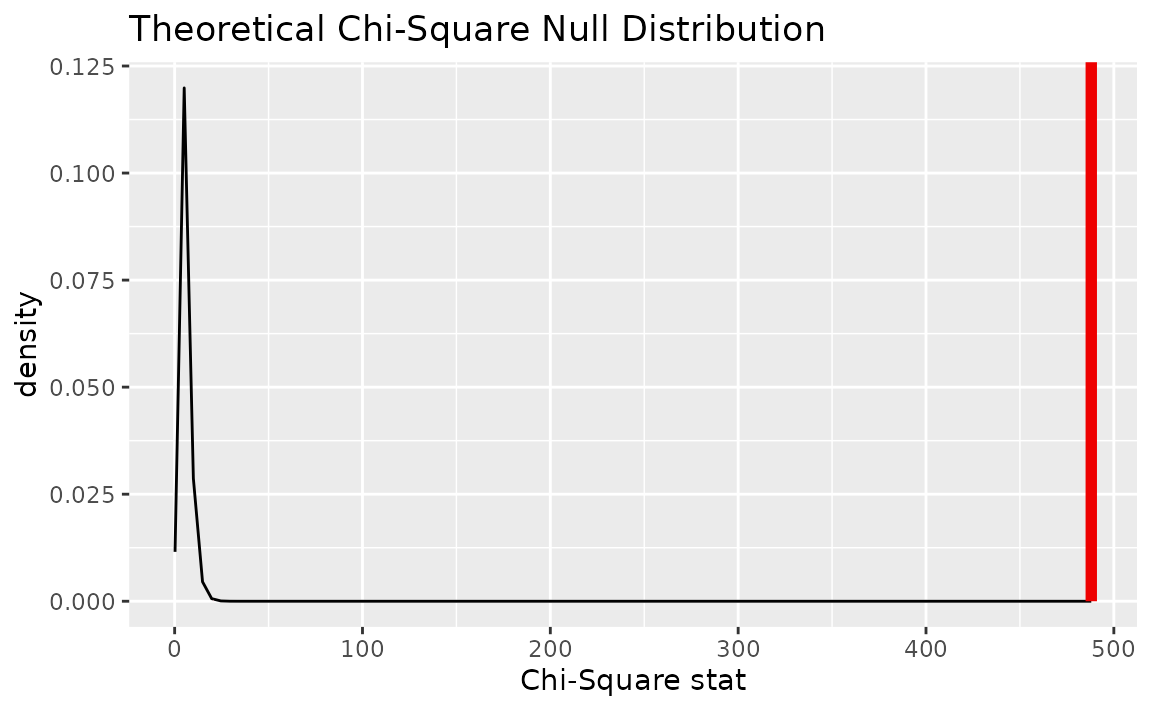

Note that the above code makes use of the randomization-based null distribution.

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = Chisq_hat, direction = "greater")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1       0

Alternatively, using the chisq_test wrapper:

chisq_test(gss, 
           response = finrela,
           p = c("far below average" = 1/6,
                 "below average" = 1/6,
                 "average" = 1/6,
                 "above average" = 1/6,
                 "far above average" = 1/6,
                 "DK" = 1/6))

## # A tibble: 1 × 3
##   statistic chisq_df   p_value
##       <dbl>    <dbl>     <dbl>
## 1      488.        5 3.13e-103

Two categorical (>2 level): Chi-squared test of independence

Calculating the observed statistic,

Chisq_hat <- gss %>%
  specify(formula = finrela ~ sex) %>% 
  hypothesize(null = "independence") %>%
  calculate(stat = "Chisq")

Alternatively, using the observe() wrapper to calculate the observed statistic,

Chisq_hat <- gss %>%
  observe(formula = finrela ~ sex, stat = "Chisq")

Then, generating the null distribution,

null_dist <- gss %>%
  specify(finrela ~ sex) %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000, type = "permute") %>% 
  calculate(stat = "Chisq")

Alternatively, finding the null distribution using theoretical methods using the assume() verb,

null_dist_theory <- gss %>%
  specify(finrela ~ sex) %>%
  assume(distribution = "Chisq")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = Chisq_hat, direction = "greater")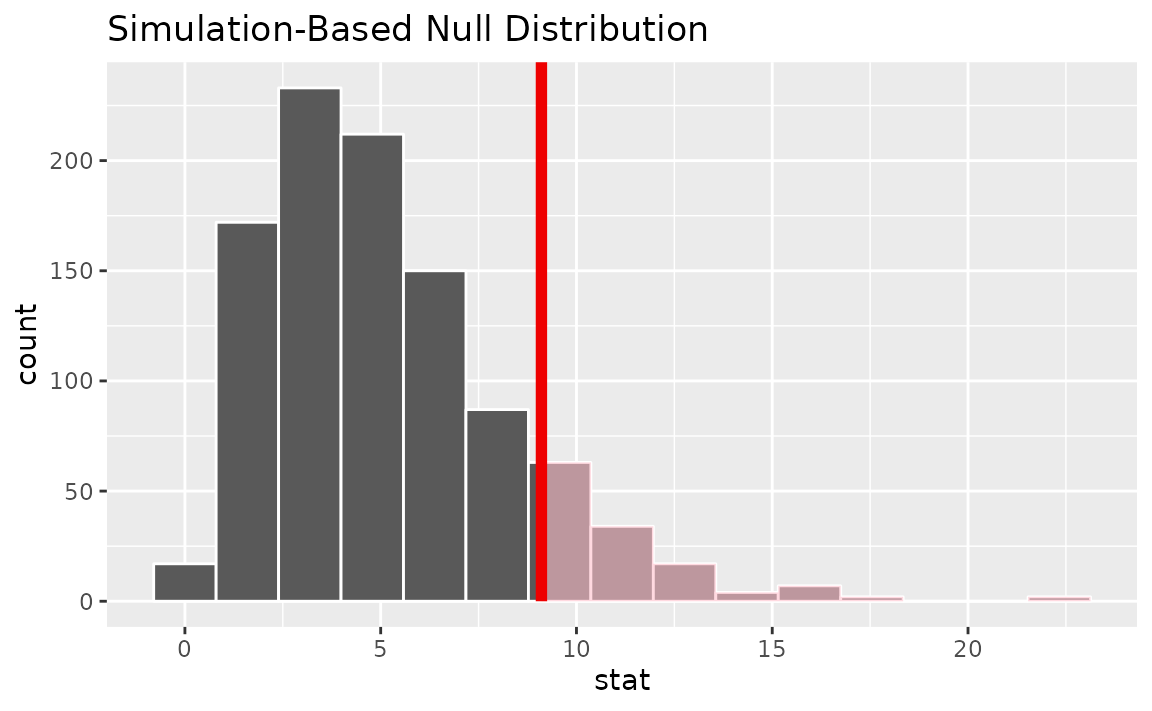

Alternatively, visualizing the observed statistic using the theory-based null distribution,

visualize(null_dist_theory) +
  shade_p_value(obs_stat = Chisq_hat, direction = "greater")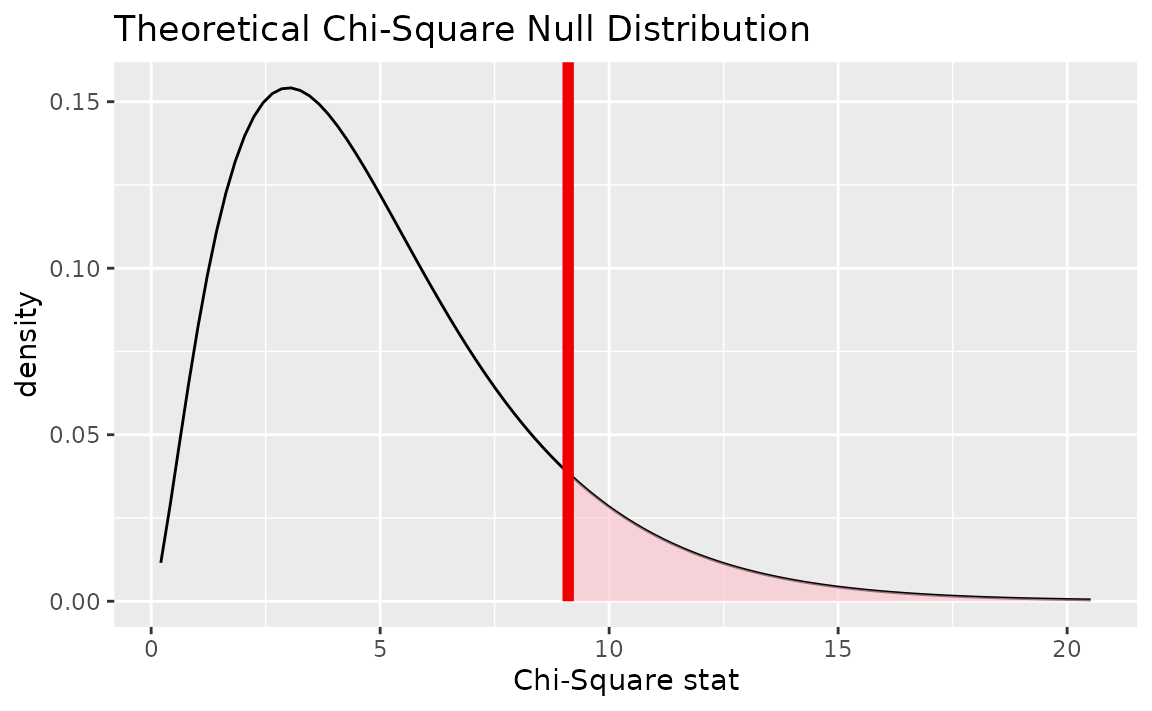

Alternatively, visualizing the observed statistic using both of the null distributions,

visualize(null_dist, method = "both") +
  shade_p_value(obs_stat = Chisq_hat, direction = "greater")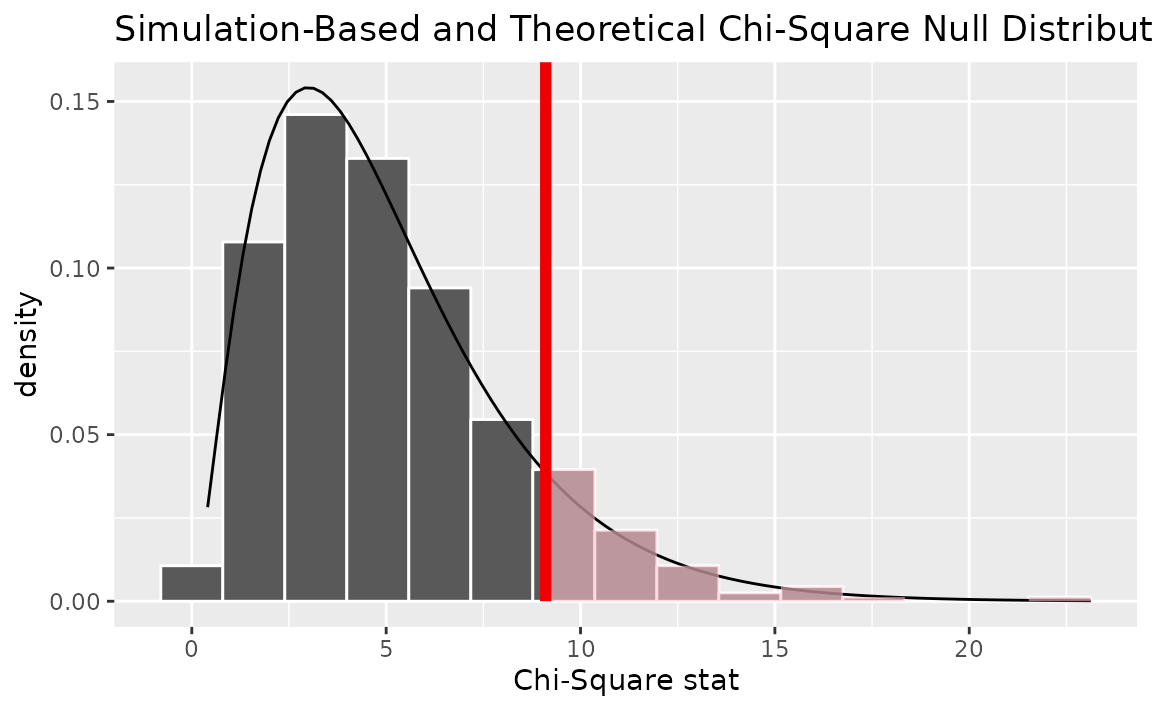

Note that the above code makes use of the randomization-based null distribution.

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = Chisq_hat, direction = "greater")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.118

Alternatively, using the wrapper to carry out the test,

gss %>%
  chisq_test(formula = finrela ~ sex)

## # A tibble: 1 × 3
##   statistic chisq_df p_value
##       <dbl>    <int>   <dbl>
## 1      9.11        5   0.105

One numerical variable, one categorical (2 levels) (diff in means)

Calculating the observed statistic,

d_hat <- gss %>% 
  specify(age ~ college) %>% 
  calculate(stat = "diff in means", order = c("degree", "no degree"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

d_hat <- gss %>% 
  observe(age ~ college,
          stat = "diff in means", order = c("degree", "no degree"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(age ~ college) %>%
  hypothesize(null = "independence") %>%
  generate(reps = 1000, type = "permute") %>%
  calculate(stat = "diff in means", order = c("degree", "no degree"))

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = d_hat, direction = "two-sided")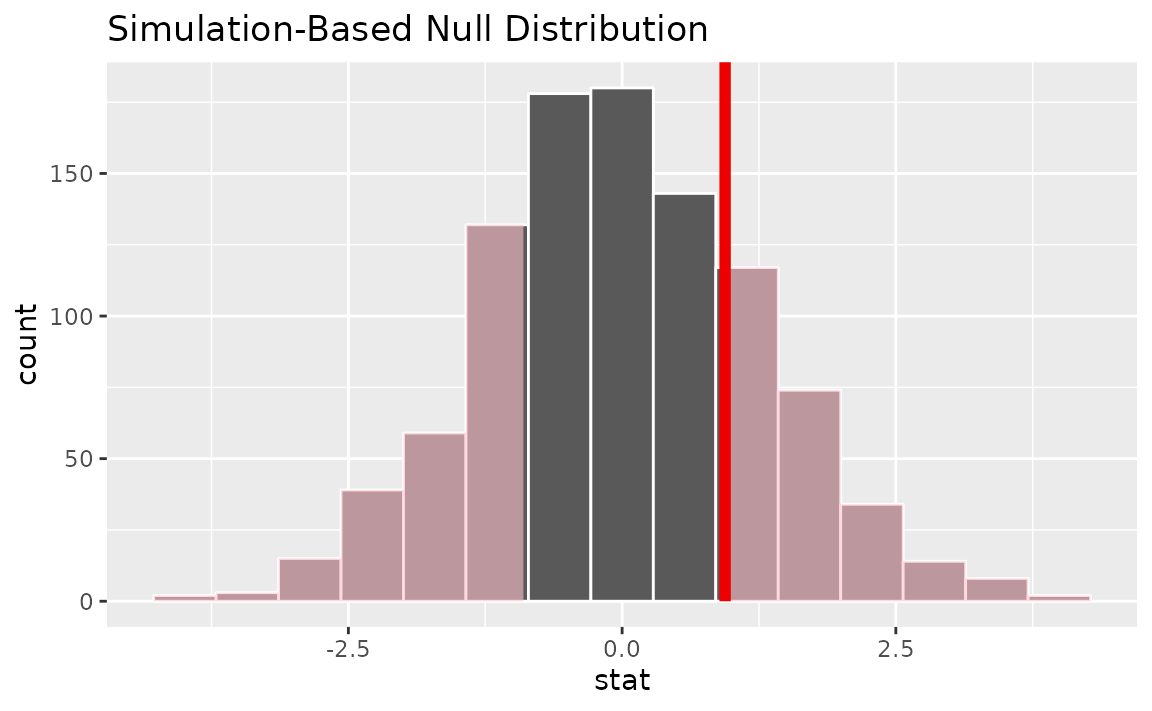

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = d_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1    0.46

One numerical variable, one categorical (2 levels) (t)

Finding the standardized observed statistic,

t_hat <- gss %>% 
  specify(age ~ college) %>% 
  hypothesize(null = "independence") %>%
  calculate(stat = "t", order = c("degree", "no degree"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

t_hat <- gss %>% 
  observe(age ~ college,
          stat = "t", order = c("degree", "no degree"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(age ~ college) %>%
  hypothesize(null = "independence") %>%
  generate(reps = 1000, type = "permute") %>%
  calculate(stat = "t", order = c("degree", "no degree"))

Alternatively, finding the null distribution using theoretical methods using the assume() verb,

null_dist_theory <- gss %>%
  specify(age ~ college) %>%
  assume("t")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = t_hat, direction = "two-sided")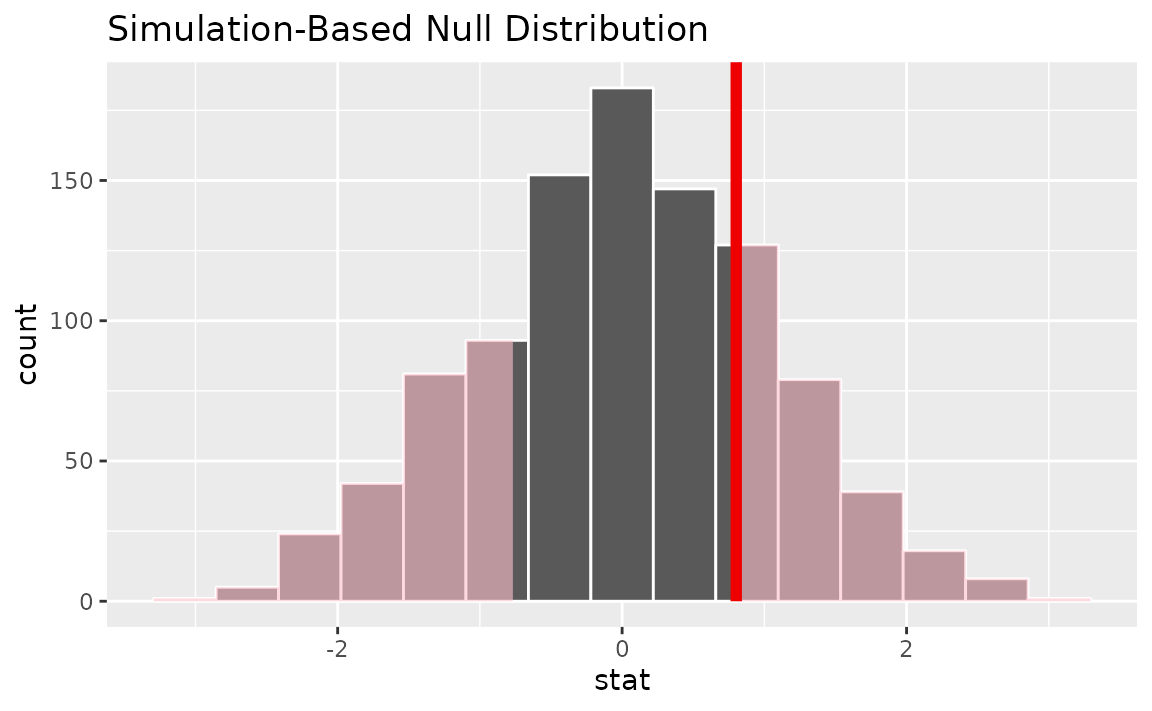

Alternatively, visualizing the observed statistic using the theory-based null distribution,

visualize(null_dist_theory) +
  shade_p_value(obs_stat = t_hat, direction = "two-sided")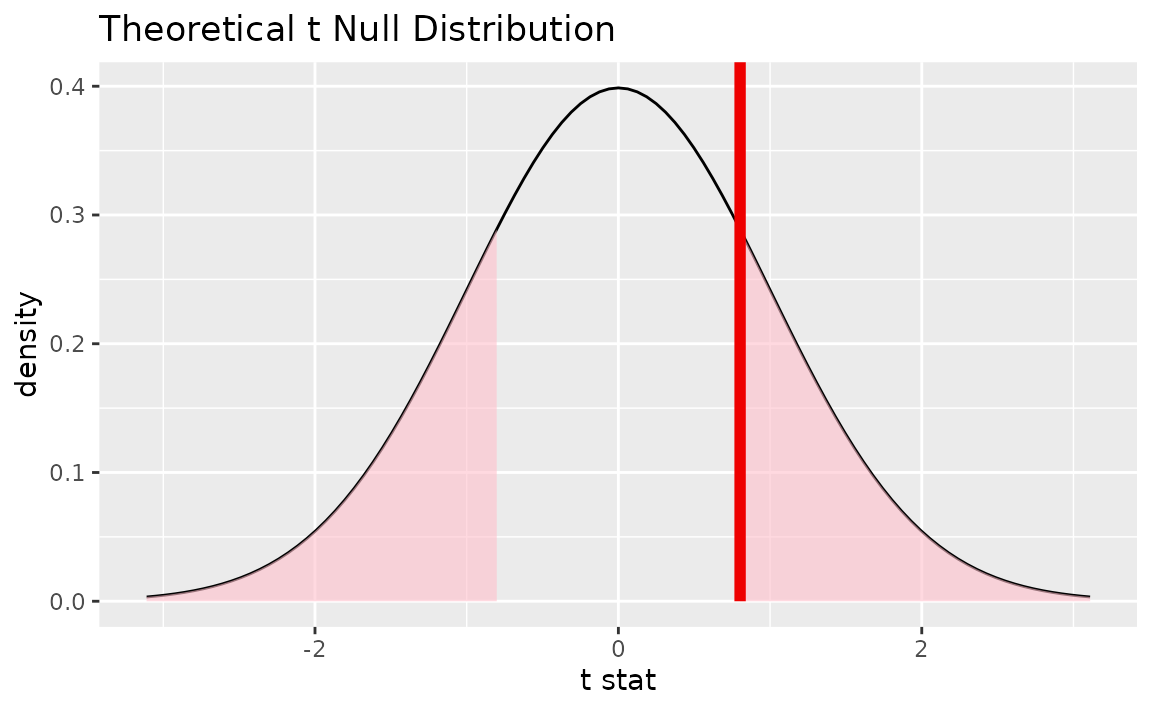

Alternatively, visualizing the observed statistic using both of the null distributions,

visualize(null_dist, method = "both") +
  shade_p_value(obs_stat = t_hat, direction = "two-sided")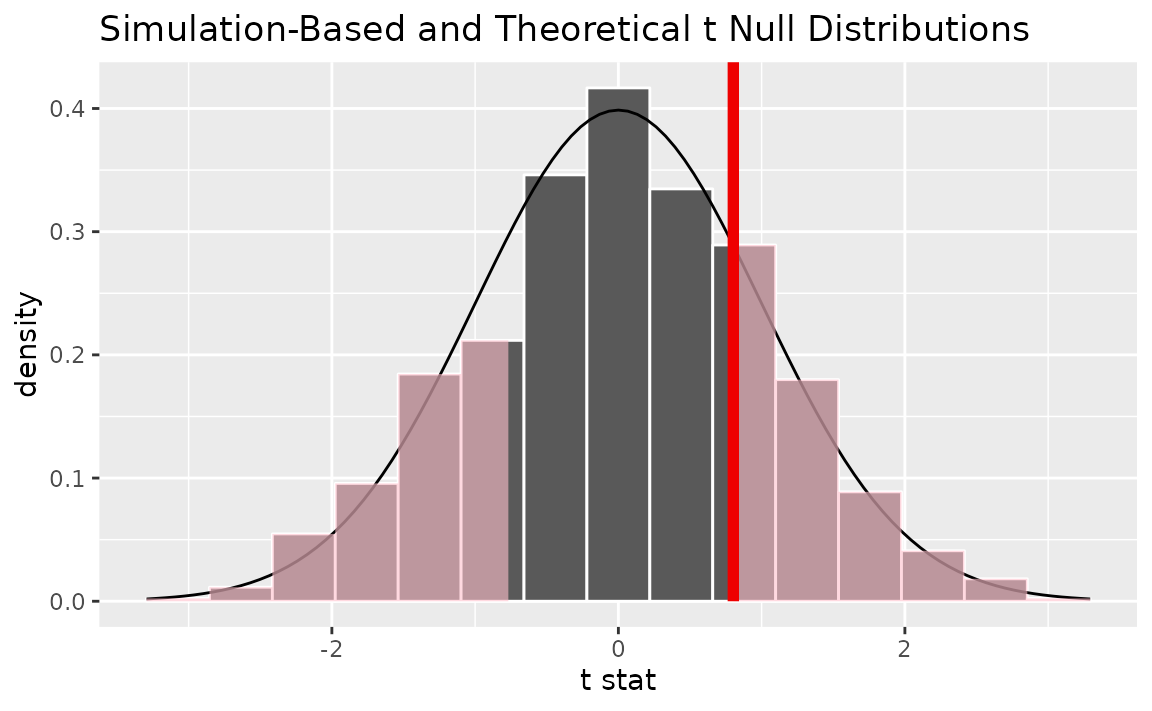

Note that the above code makes use of the randomization-based null distribution.

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = t_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.442

Note the similarities in this plot and the previous one.

One numerical variable, one categorical (2 levels) (diff in medians)

Calculating the observed statistic,

d_hat <- gss %>% 
  specify(age ~ college) %>% 
  calculate(stat = "diff in medians", order = c("degree", "no degree"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

d_hat <- gss %>% 
  observe(age ~ college,
          stat = "diff in medians", order = c("degree", "no degree"))

Then, generating the null distribution,

null_dist <- gss %>%
  specify(age ~ college) %>% # alt: response = age, explanatory = season
  hypothesize(null = "independence") %>%
  generate(reps = 1000, type = "permute") %>%
  calculate(stat = "diff in medians", order = c("degree", "no degree"))

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = d_hat, direction = "two-sided")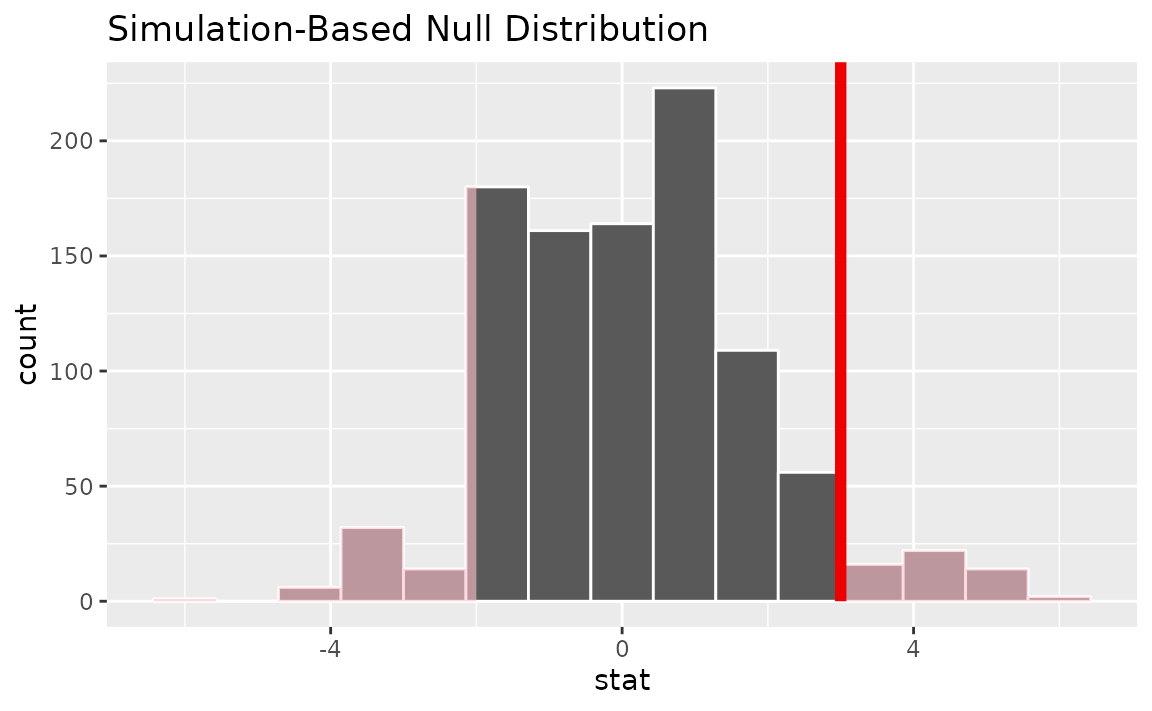

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = d_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.172

One numerical, one categorical (>2 levels) - ANOVA

Calculating the observed statistic,

F_hat <- gss %>% 
  specify(age ~ partyid) %>%
  calculate(stat = "F")

Alternatively, using the observe() wrapper to calculate the observed statistic,

F_hat <- gss %>% 
  observe(age ~ partyid, stat = "F")

Then, generating the null distribution,

null_dist <- gss %>%
   specify(age ~ partyid) %>%
   hypothesize(null = "independence") %>%
   generate(reps = 1000, type = "permute") %>%
   calculate(stat = "F")

Alternatively, finding the null distribution using theoretical methods using the assume() verb,

null_dist_theory <- gss %>%
   specify(age ~ partyid) %>%
   hypothesize(null = "independence") %>%
   assume(distribution = "F")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = F_hat, direction = "greater")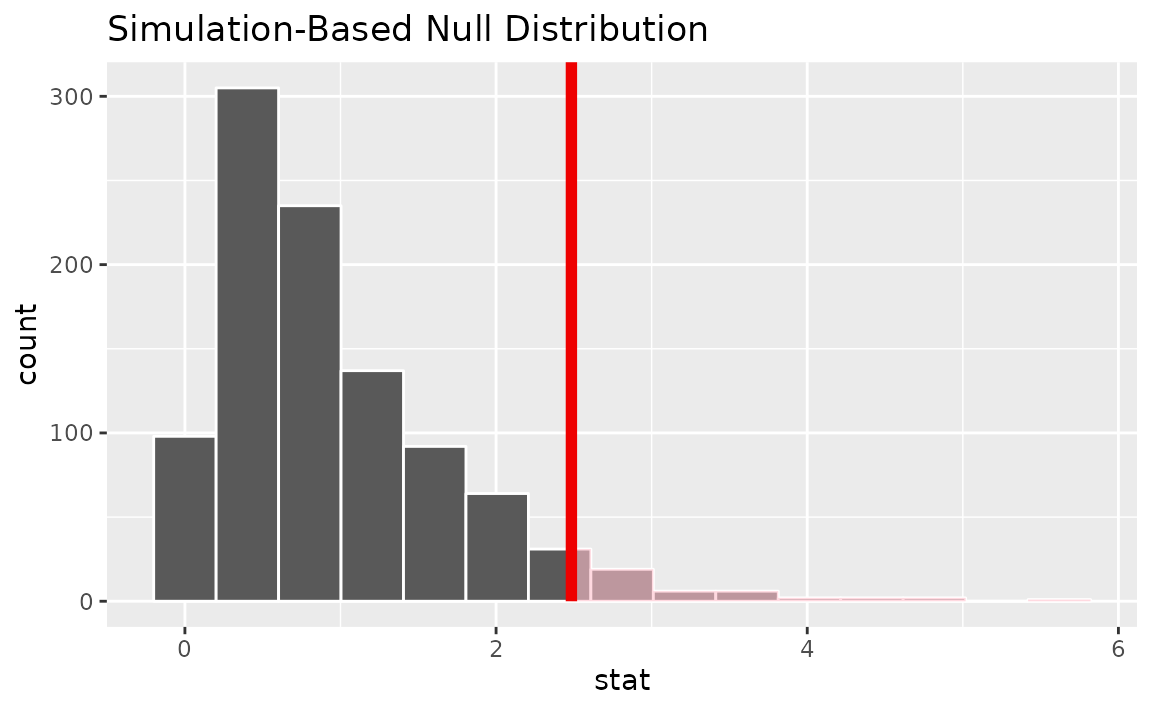

Alternatively, visualizing the observed statistic using the theory-based null distribution,

visualize(null_dist_theory) +
  shade_p_value(obs_stat = F_hat, direction = "greater")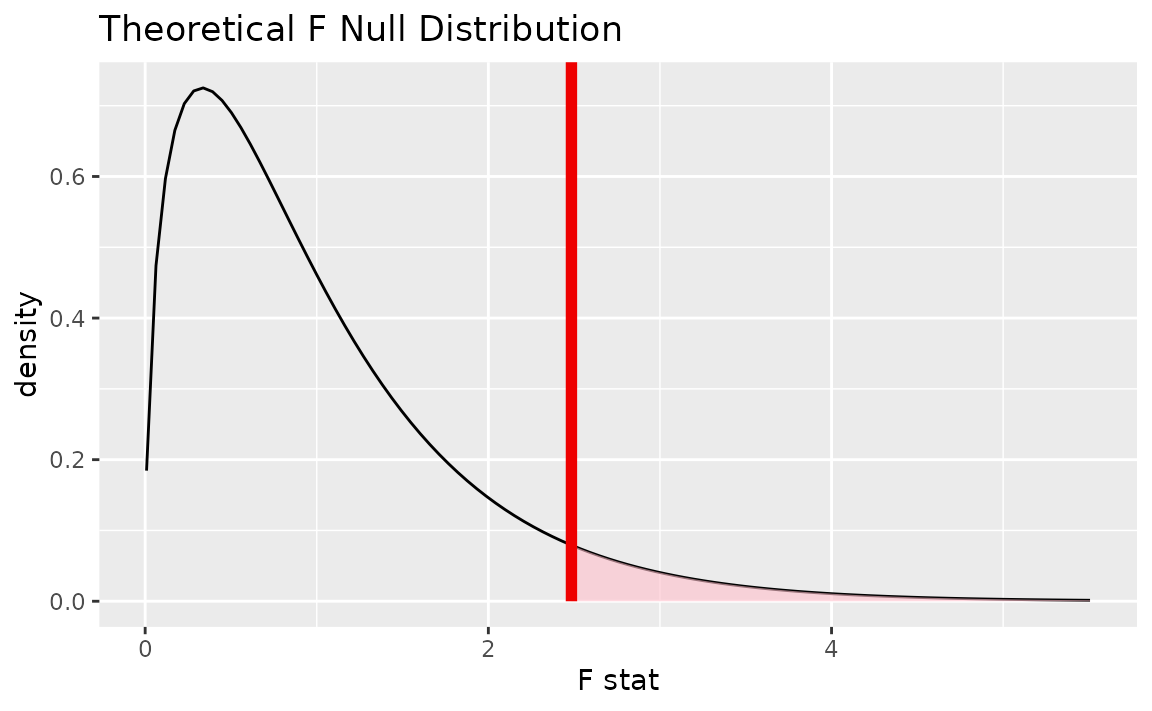

Alternatively, visualizing the observed statistic using both of the null distributions,

visualize(null_dist, method = "both") +
  shade_p_value(obs_stat = F_hat, direction = "greater")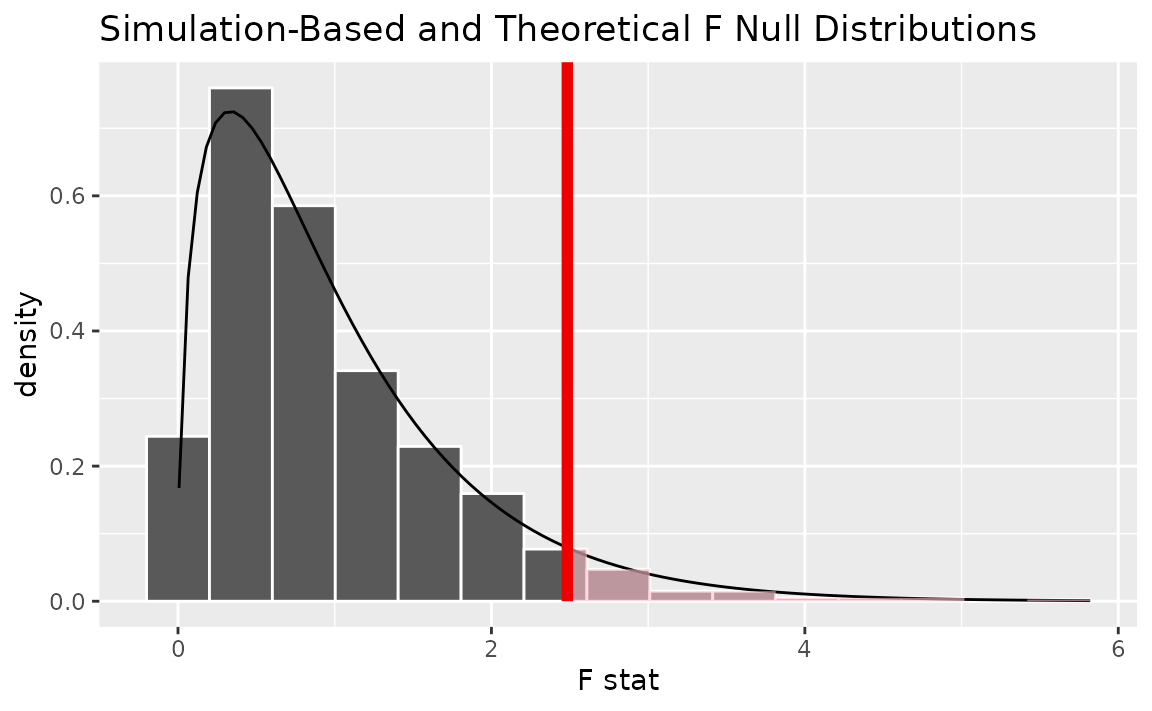

Note that the above code makes use of the randomization-based null distribution.

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = F_hat, direction = "greater")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.045

Two numerical vars - SLR

Calculating the observed statistic,

slope_hat <- gss %>% 
  specify(hours ~ age) %>% 
  calculate(stat = "slope")

Alternatively, using the observe() wrapper to calculate the observed statistic,

slope_hat <- gss %>% 
  observe(hours ~ age, stat = "slope")

Then, generating the null distribution,

null_dist <- gss %>%
   specify(hours ~ age) %>% 
   hypothesize(null = "independence") %>%
   generate(reps = 1000, type = "permute") %>%
   calculate(stat = "slope")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = slope_hat, direction = "two-sided")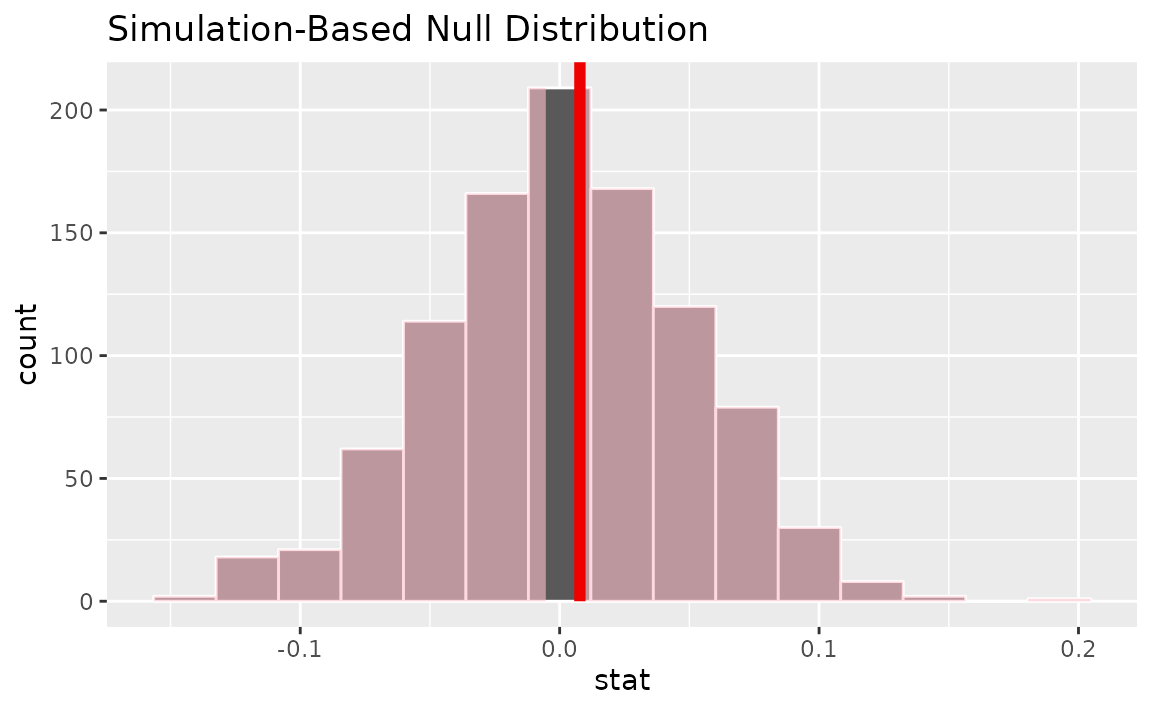

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = slope_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.902

Two numerical vars - correlation

Calculating the observed statistic,

correlation_hat <- gss %>% 
  specify(hours ~ age) %>% 
  calculate(stat = "correlation")

Alternatively, using the observe() wrapper to calculate the observed statistic,

correlation_hat <- gss %>% 
  observe(hours ~ age, stat = "correlation")

Then, generating the null distribution,

null_dist <- gss %>%
   specify(hours ~ age) %>% 
   hypothesize(null = "independence") %>%
   generate(reps = 1000, type = "permute") %>%
   calculate(stat = "correlation")

Visualizing the observed statistic alongside the null distribution,

visualize(null_dist) +
  shade_p_value(obs_stat = correlation_hat, direction = "two-sided")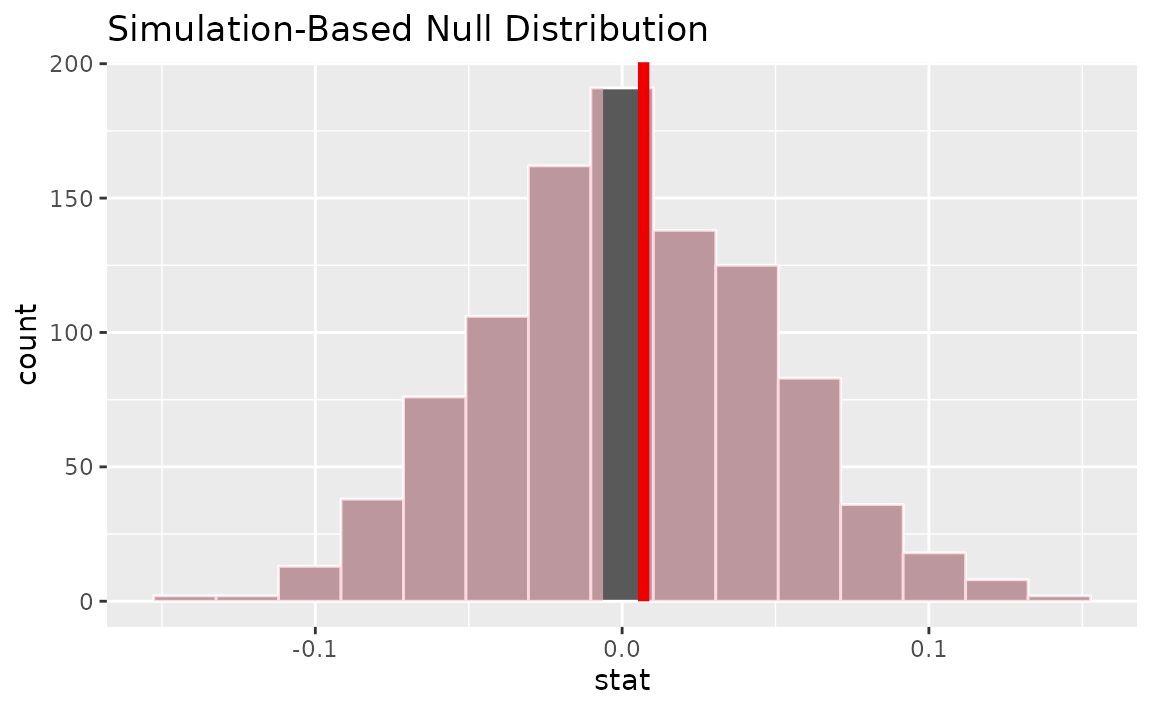

Calculating the p-value from the null distribution and observed statistic,

null_dist %>%
  get_p_value(obs_stat = correlation_hat, direction = "two-sided")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.878

Two numerical vars - SLR (t)

Not currently implemented since \(t\) could refer to standardized slope or standardized correlation.

Multiple explanatory variables

Calculating the observed fit,

obs_fit <- gss %>%
  specify(hours ~ age + college) %>%
  fit()

Generating a distribution of fits with the response variable permuted,

null_dist <- gss %>%
  specify(hours ~ age + college) %>%
  hypothesize(null = "independence") %>%
  generate(reps = 1000, type = "permute") %>%
  fit()

Generating a distribution of fits where each explanatory variable is permuted independently,

null_dist2 <- gss %>%
  specify(hours ~ age + college) %>%
  hypothesize(null = "independence") %>%
  generate(reps = 1000, type = "permute", variables = c(age, college)) %>%
  fit()

Visualizing the observed fit alongside the null fits,

visualize(null_dist) +
  shade_p_value(obs_stat = obs_fit, direction = "two-sided")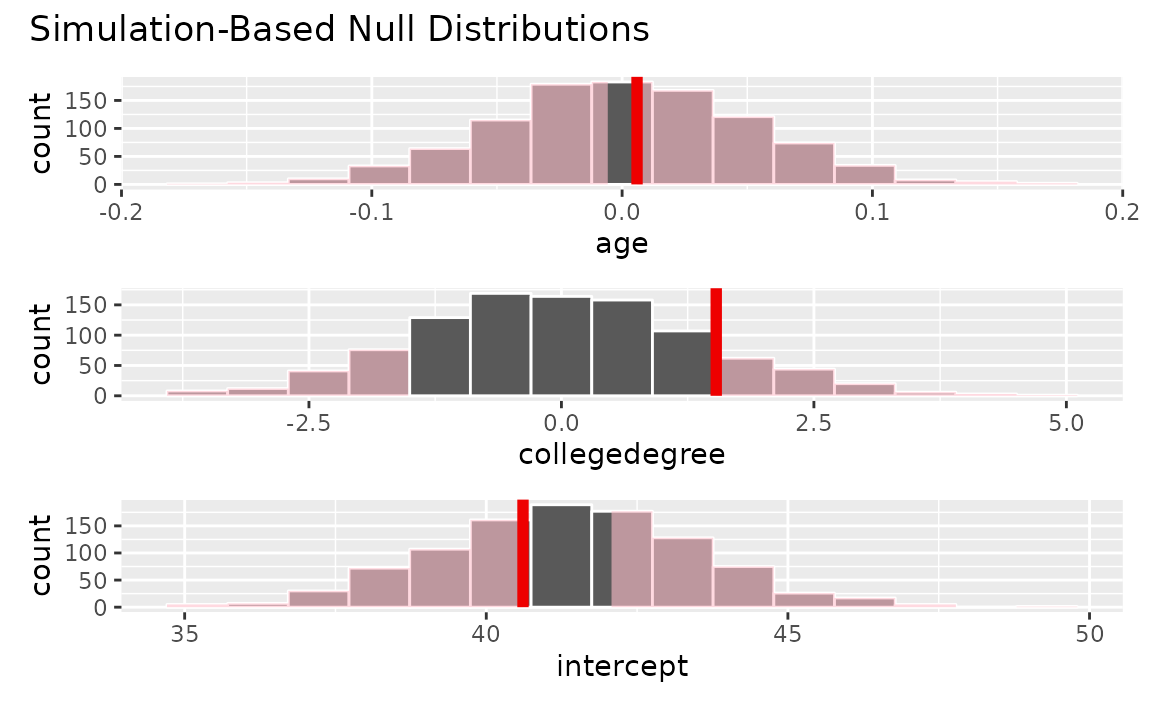

Calculating p-values from the null distribution and observed fit,

null_dist %>%
  get_p_value(obs_stat = obs_fit, direction = "two-sided")

## # A tibble: 3 × 2
##   term          p_value
##   <chr>           <dbl>
## 1 age             0.914
## 2 collegedegree   0.266
## 3 intercept       0.734

Note that this fit()-based workflow can be applied to use cases with differing numbers of explanatory variables and explanatory variable types.

Confidence intervals

One numerical (one mean)

Finding the observed statistic,

x_bar <- gss %>% 
  specify(response = hours) %>%
  calculate(stat = "mean")

Alternatively, using the observe() wrapper to calculate the observed statistic,

x_bar <- gss %>% 
  observe(response = hours, stat = "mean")

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
   specify(response = hours) %>%
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "mean")

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)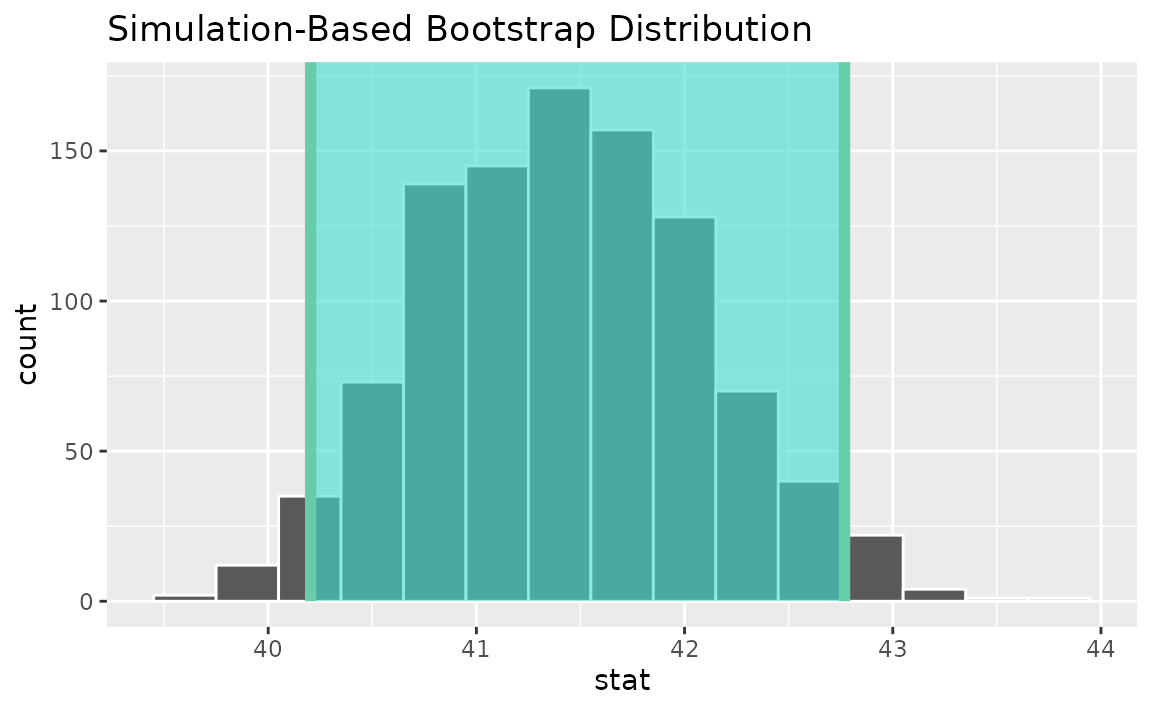

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- get_ci(boot_dist, type = "se", point_estimate = x_bar)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)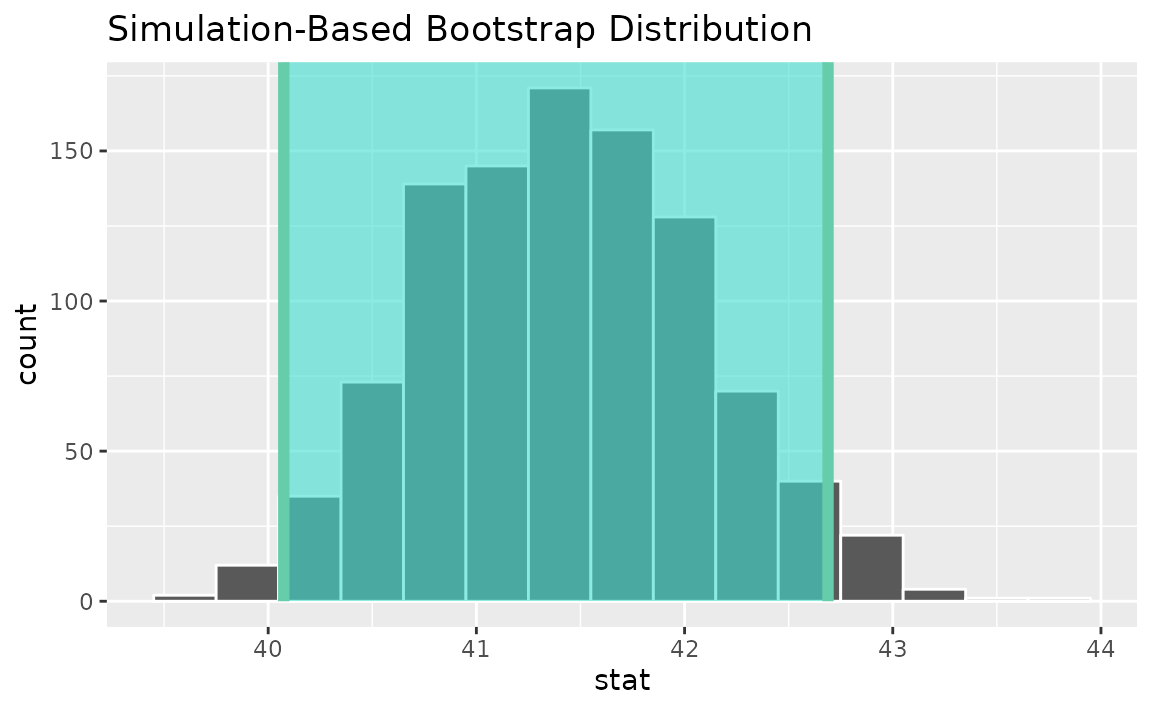

Instead of a simulation-based bootstrap distribution, we can also define a theory-based sampling distribution,

sampling_dist <- gss %>%
   specify(response = hours) %>%
   assume(distribution = "t")

Visualization and calculation of confidence intervals interfaces in the same way as with the simulation-based distribution,

theor_ci <- get_ci(sampling_dist, point_estimate = x_bar)

theor_ci

## # A tibble: 1 × 2
##   lower_ci upper_ci
##      <dbl>    <dbl>
## 1     40.1     42.7

visualize(sampling_dist) +
  shade_confidence_interval(endpoints = theor_ci)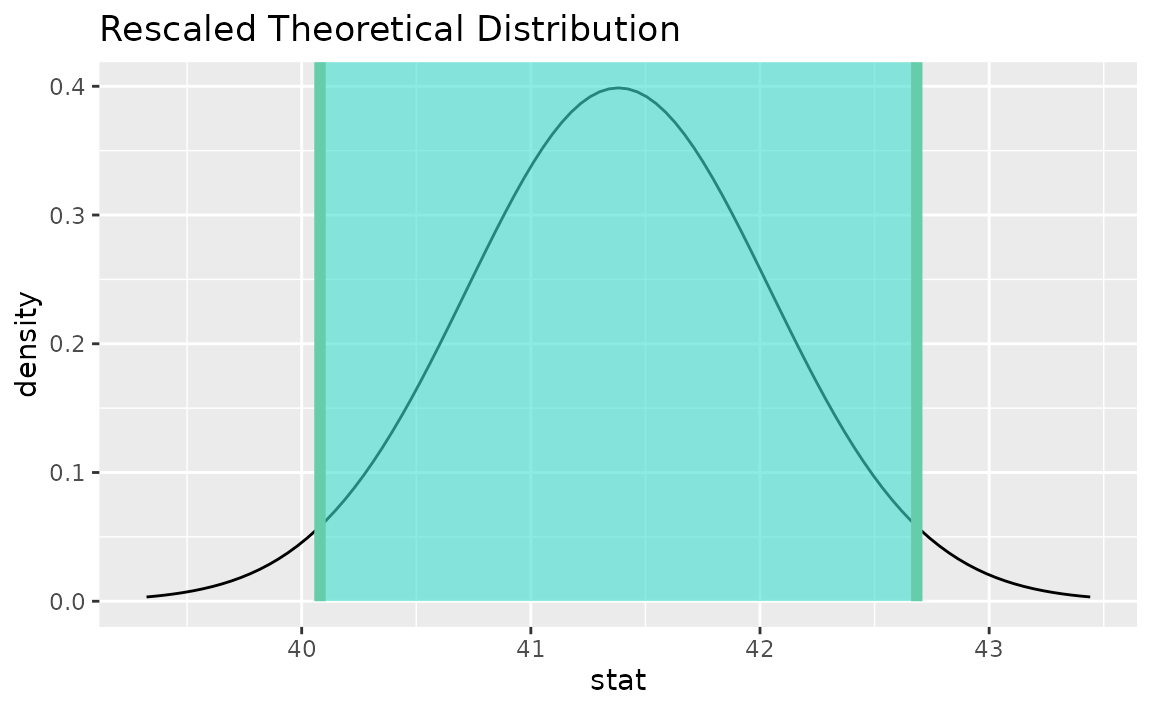

Note that the t distribution is recentered and rescaled to lie on the scale of the observed data. infer does not support confidence intervals on means via the z distribution.

One numerical (one mean - standardized)

Finding the observed statistic,

t_hat <- gss %>% 
  specify(response = hours) %>%
  hypothesize(null = "point", mu = 40) %>%
  calculate(stat = "t")

Alternatively, using the observe() wrapper to calculate the observed statistic,

t_hat <- gss %>% 
  observe(response = hours,
          null = "point", mu = 40,
          stat = "t")

Then, generating the bootstrap distribution,

boot_dist <- gss %>%
   specify(response = hours) %>%
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "t")

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)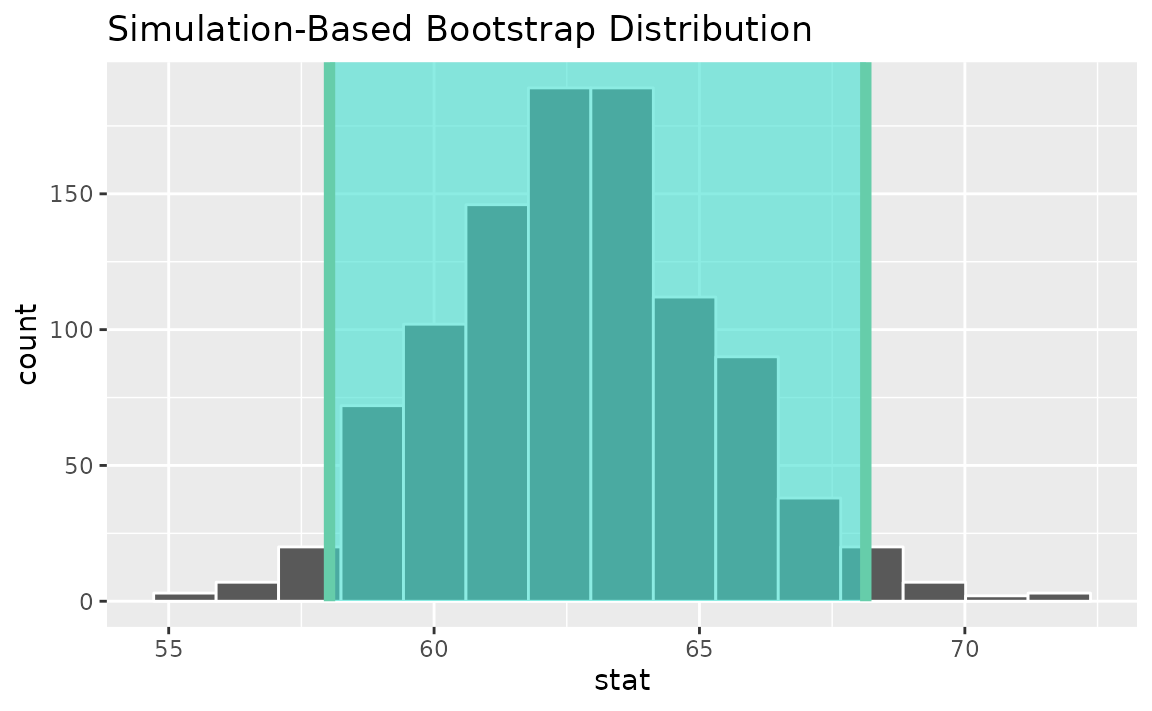

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = t_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)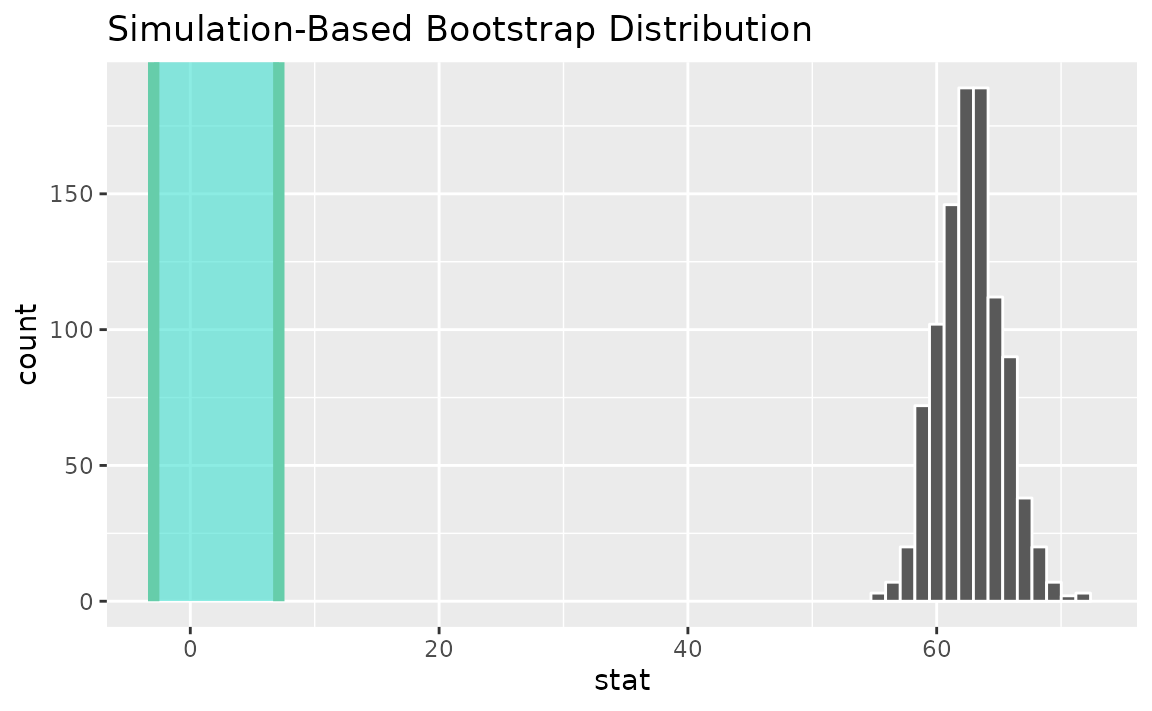

See the above subsection (one mean) for a theory-based approach. Note that infer does not support confidence intervals on means via the z distribution.

One categorical (one proportion)

Finding the observed statistic,

p_hat <- gss %>% 
   specify(response = sex, success = "female") %>%
   calculate(stat = "prop")

Alternatively, using the observe() wrapper to calculate the observed statistic,

p_hat <- gss %>% 
   observe(response = sex, success = "female", stat = "prop")

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
 specify(response = sex, success = "female") %>%
 generate(reps = 1000, type = "bootstrap") %>%
 calculate(stat = "prop")

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)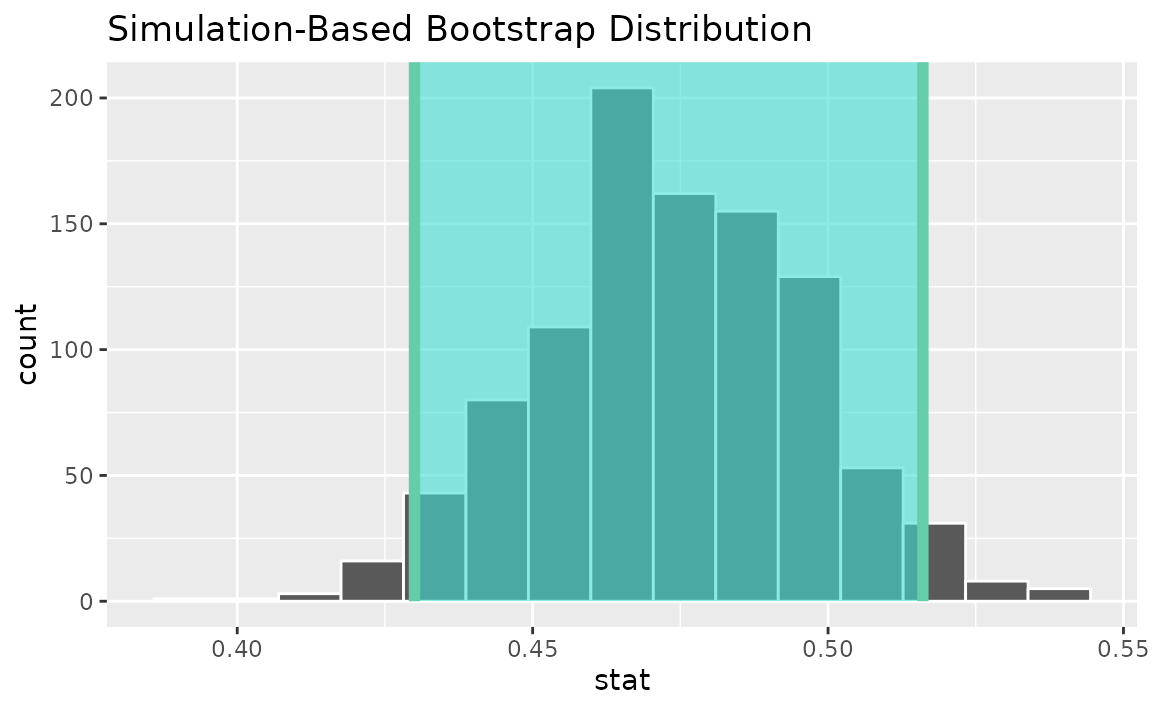

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = p_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)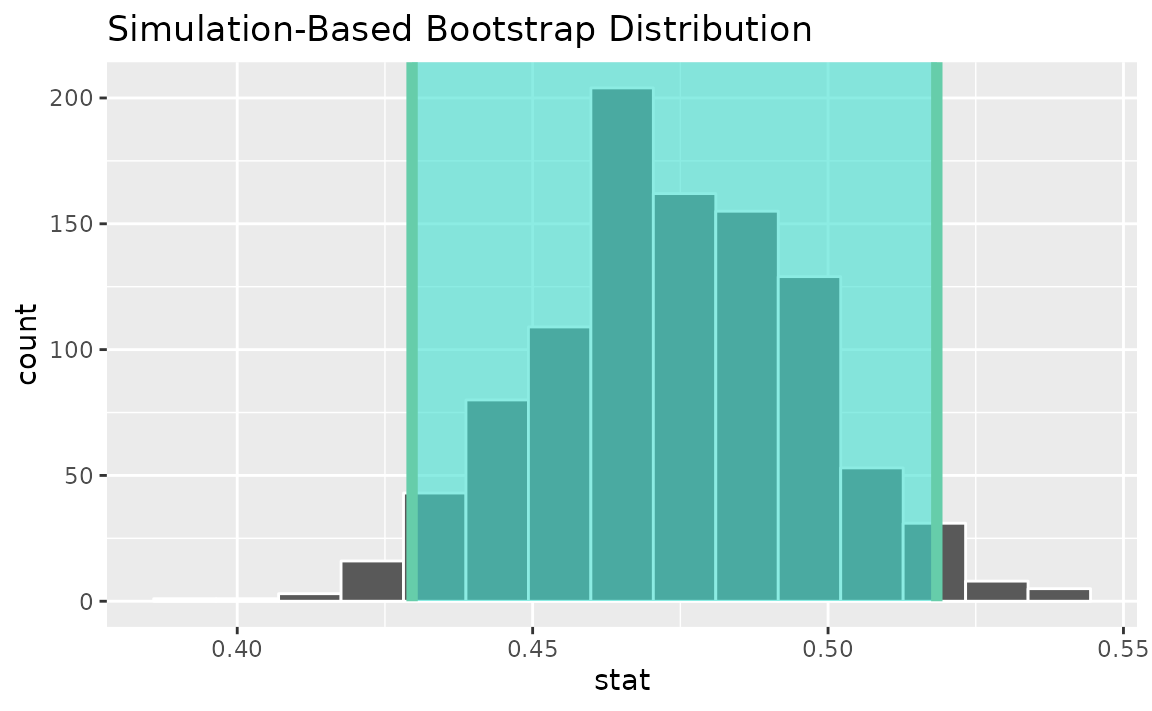

Instead of a simulation-based bootstrap distribution, we can also define a theory-based sampling distribution,

sampling_dist <- gss %>%
   specify(response = sex, success = "female") %>%
   assume(distribution = "z")

Visualization and calculation of confidence intervals interfaces in the same way as with the simulation-based distribution,

theor_ci <- get_ci(sampling_dist, point_estimate = p_hat)

theor_ci

## # A tibble: 1 × 2
##   lower_ci upper_ci
##      <dbl>    <dbl>
## 1    0.430    0.518

visualize(sampling_dist) +
  shade_confidence_interval(endpoints = theor_ci)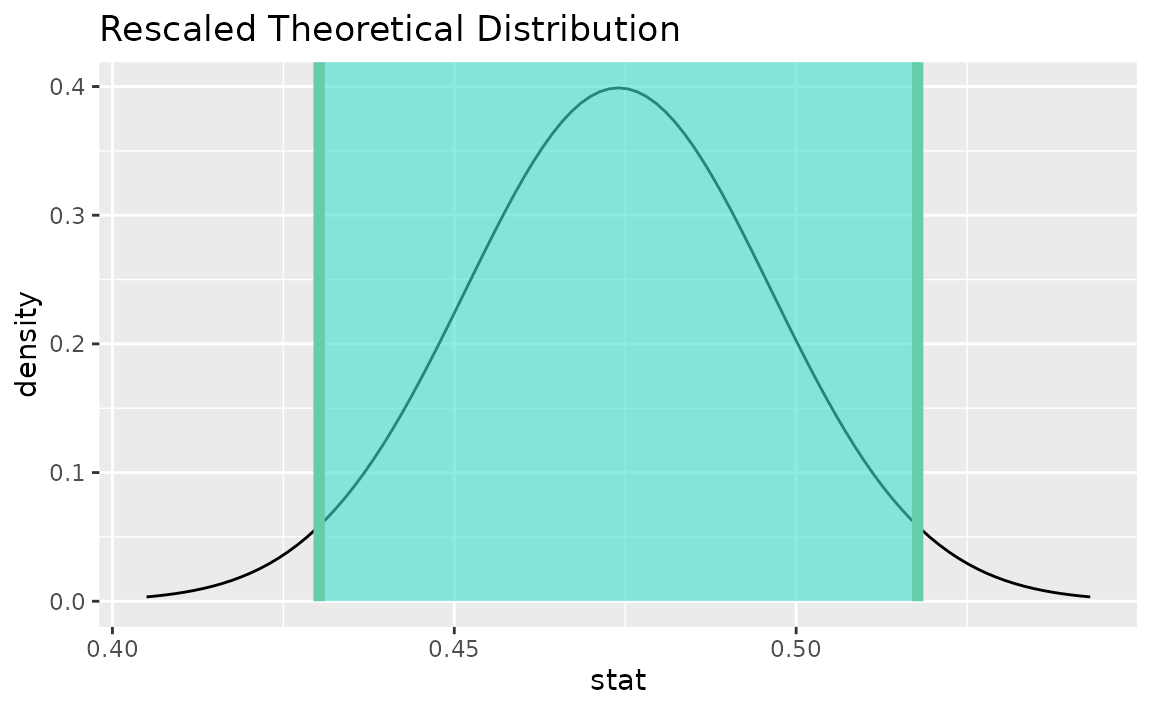

Note that the z distribution is recentered and rescaled to lie on the scale of the observed data. infer does not support confidence intervals on means via the z distribution.

One categorical variable (standardized proportion \(z\))

See the above subsection (one proportion) for a theory-based approach.

One numerical variable, one categorical (2 levels) (diff in means)

Finding the observed statistic,

d_hat <- gss %>%
  specify(hours ~ college) %>%
  calculate(stat = "diff in means", order = c("degree", "no degree"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

d_hat <- gss %>%
  observe(hours ~ college,
          stat = "diff in means", order = c("degree", "no degree"))

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
   specify(hours ~ college) %>%
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "diff in means", order = c("degree", "no degree"))

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)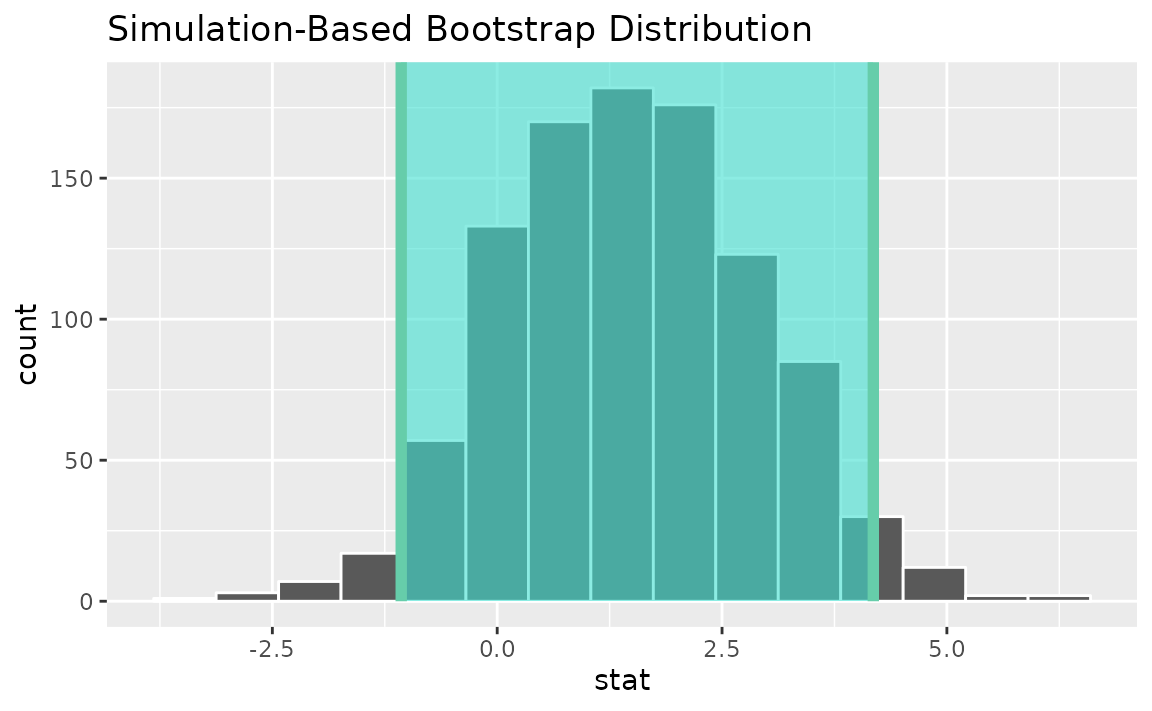

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = d_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)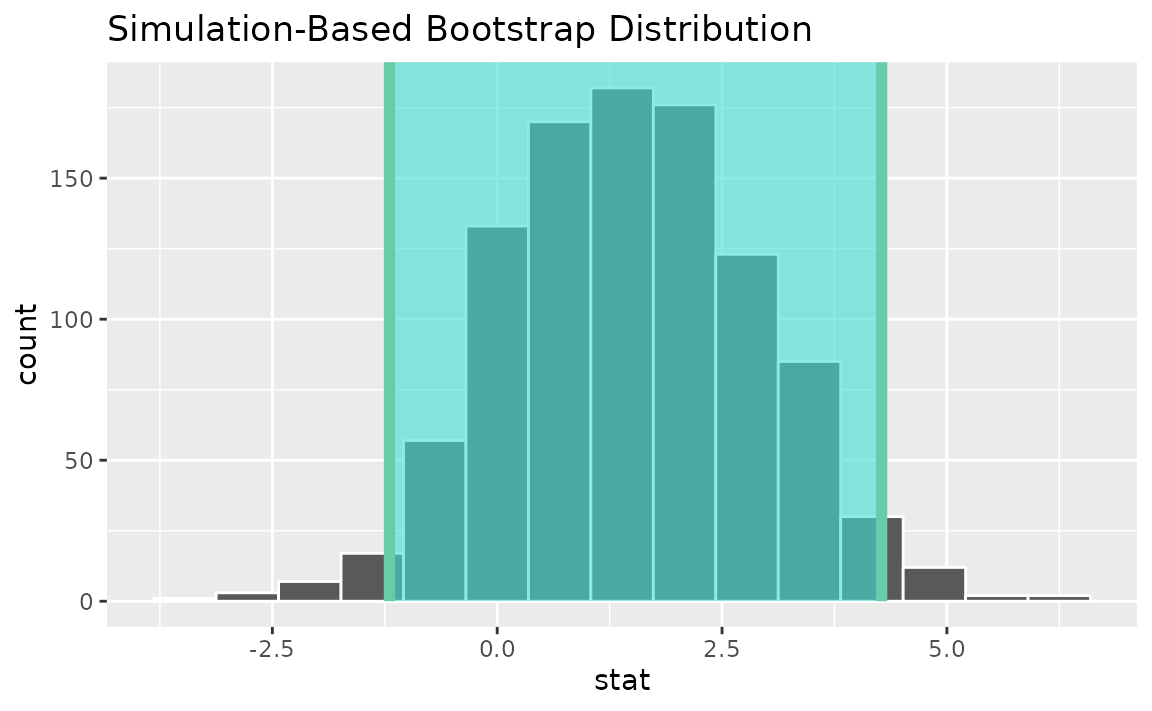

Instead of a simulation-based bootstrap distribution, we can also define a theory-based sampling distribution,

sampling_dist <- gss %>%
   specify(hours ~ college) %>%
   assume(distribution = "t")

Visualization and calculation of confidence intervals interfaces in the same way as with the simulation-based distribution,

theor_ci <- get_ci(sampling_dist, point_estimate = d_hat)

theor_ci

## # A tibble: 1 × 2
##   lower_ci upper_ci
##      <dbl>    <dbl>
## 1    -1.16     4.24

visualize(sampling_dist) +
  shade_confidence_interval(endpoints = theor_ci)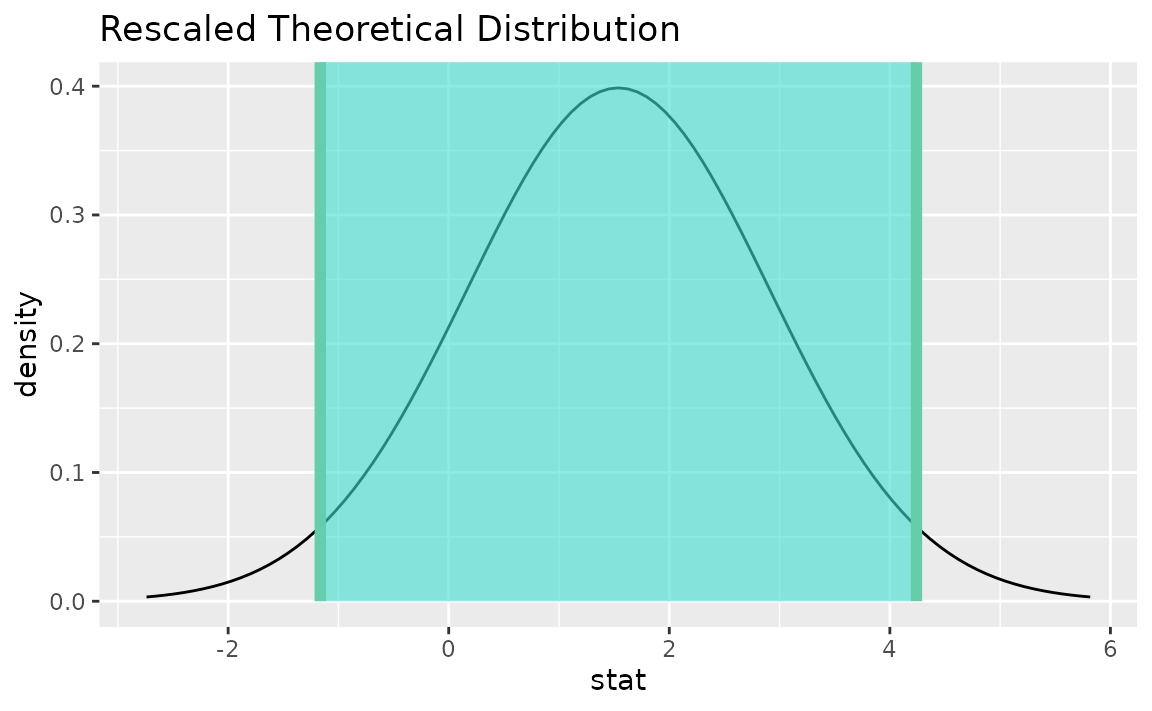

Note that the t distribution is recentered and rescaled to lie on the scale of the observed data.

infer also provides functionality to calculate ratios of means. The workflow looks similar to that for diff in means.

Finding the observed statistic,

d_hat <- gss %>%
  specify(hours ~ college) %>%
  calculate(stat = "ratio of means", order = c("degree", "no degree"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

d_hat <- gss %>%
  observe(hours ~ college,
          stat = "ratio of means", order = c("degree", "no degree"))

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
   specify(hours ~ college) %>%
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "ratio of means", order = c("degree", "no degree"))

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)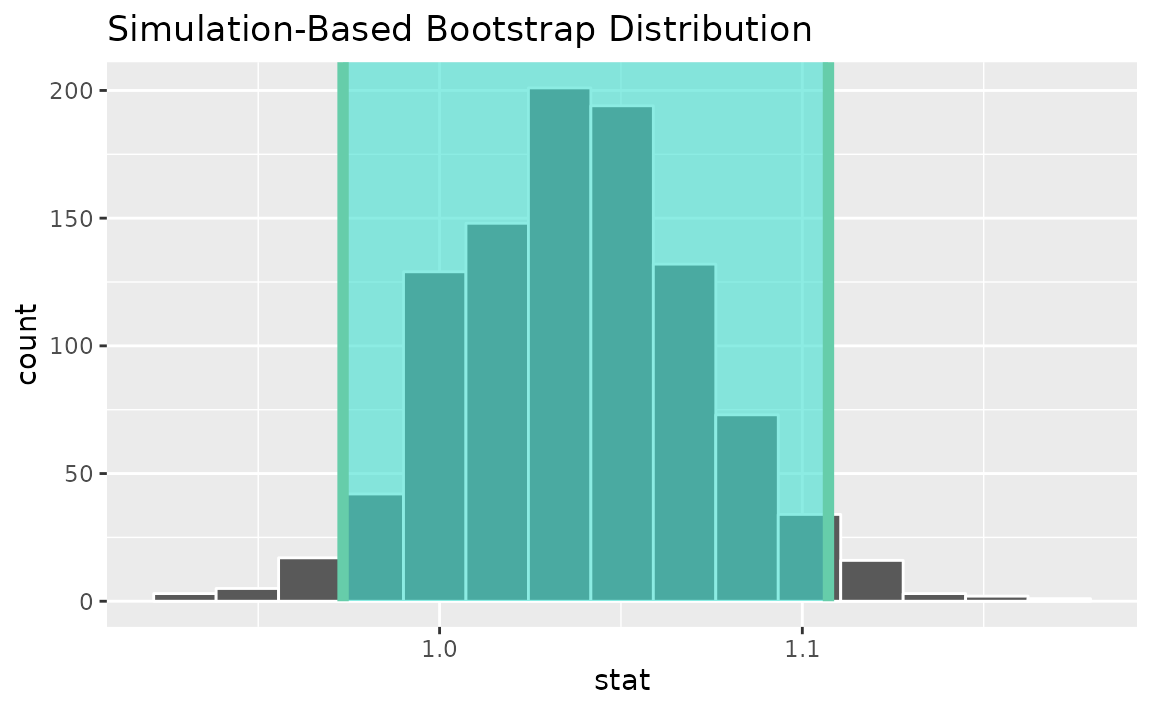

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = d_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)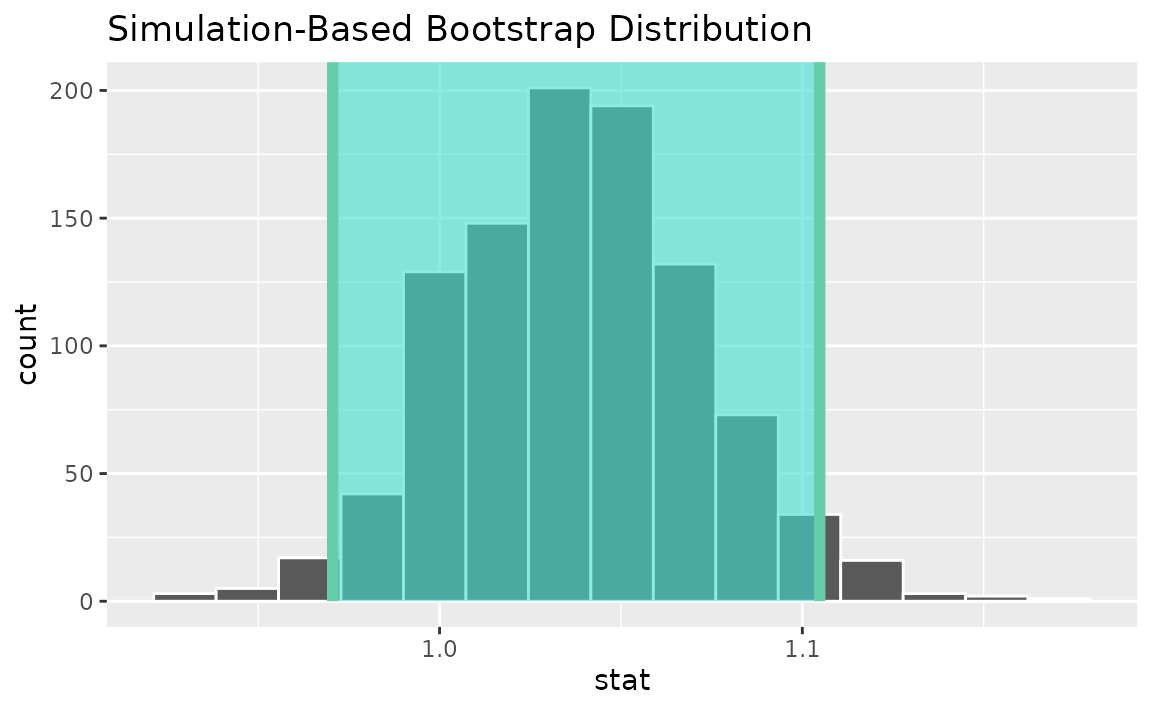

One numerical variable, one categorical (2 levels) (t)

Finding the standardized point estimate,

t_hat <- gss %>%
  specify(hours ~ college) %>%
  calculate(stat = "t", order = c("degree", "no degree"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

t_hat <- gss %>%
  observe(hours ~ college,
          stat = "t", order = c("degree", "no degree"))

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
   specify(hours ~ college) %>%
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "t", order = c("degree", "no degree"))

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)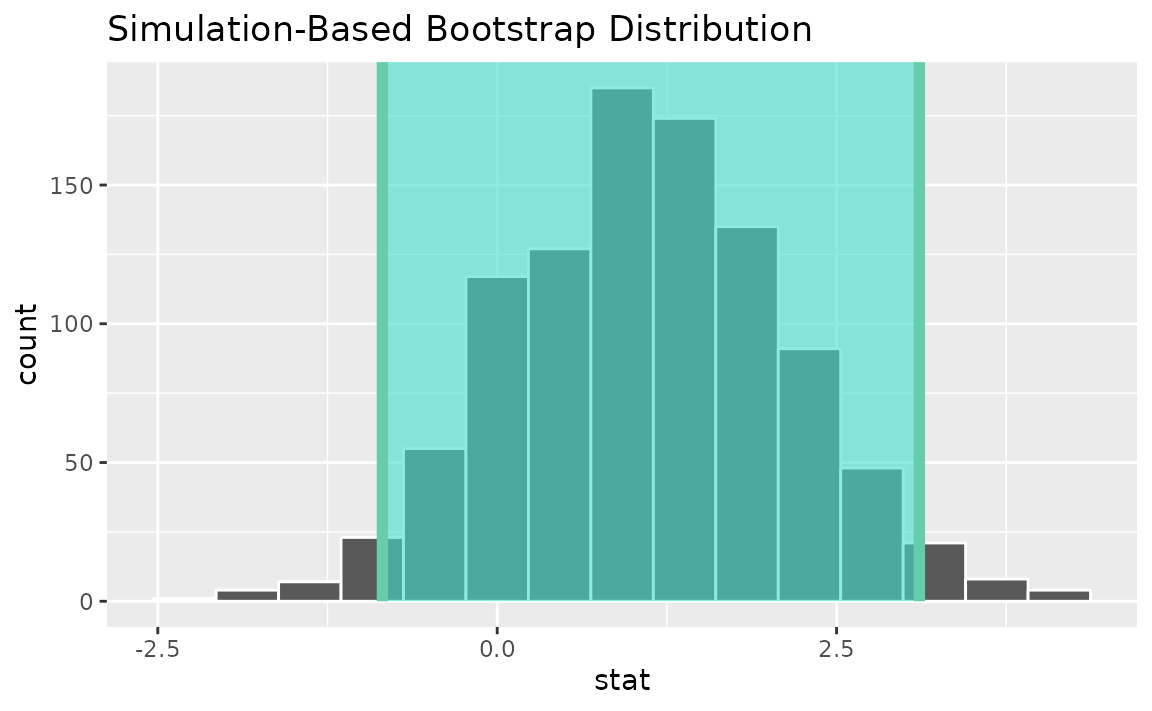

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = t_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)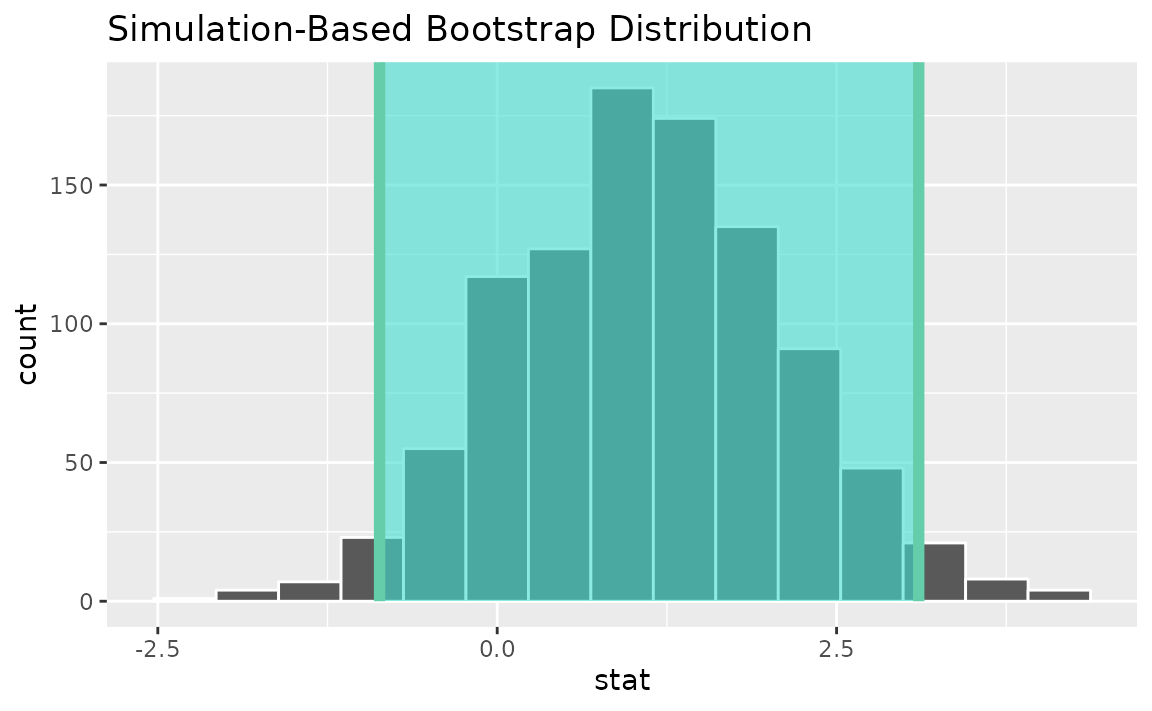

See the above subsection (diff in means) for a theory-based approach. infer does not support confidence intervals on means via the z distribution.

Two categorical variables (diff in proportions)

Finding the observed statistic,

d_hat <- gss %>% 
  specify(college ~ sex, success = "degree") %>%
  calculate(stat = "diff in props", order = c("female", "male"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

d_hat <- gss %>% 
  observe(college ~ sex, success = "degree",
          stat = "diff in props", order = c("female", "male"))

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
  specify(college ~ sex, success = "degree") %>%
  generate(reps = 1000, type = "bootstrap") %>% 
  calculate(stat = "diff in props", order = c("female", "male"))

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)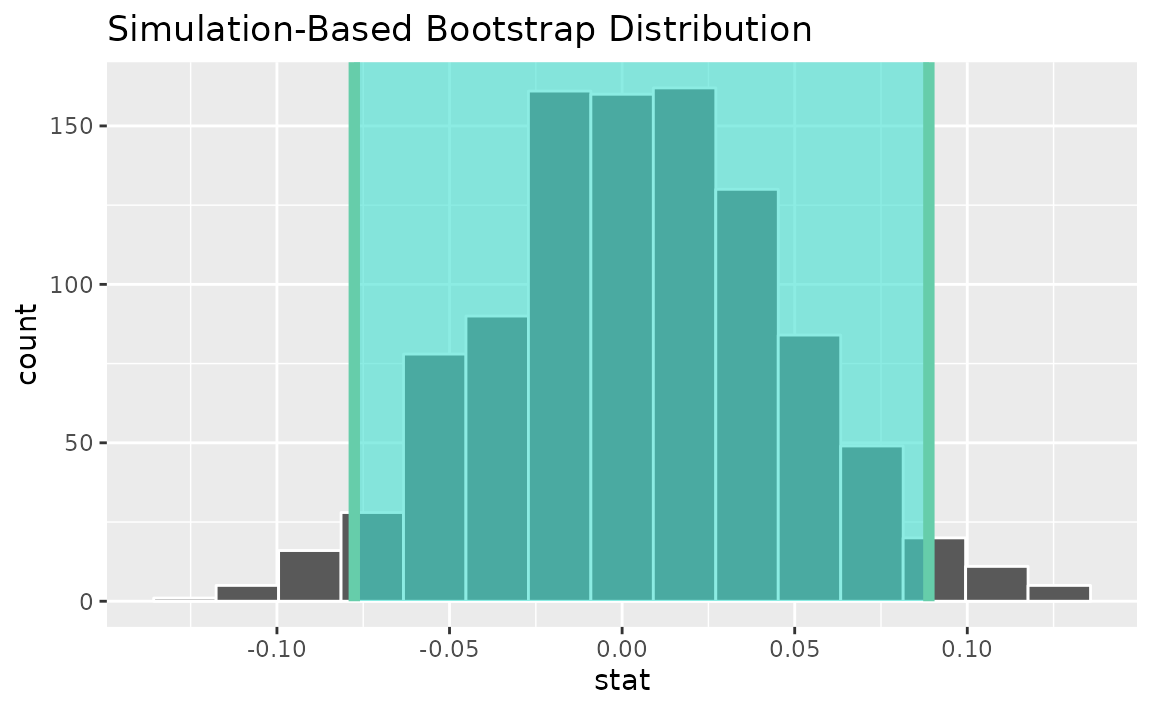

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = d_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)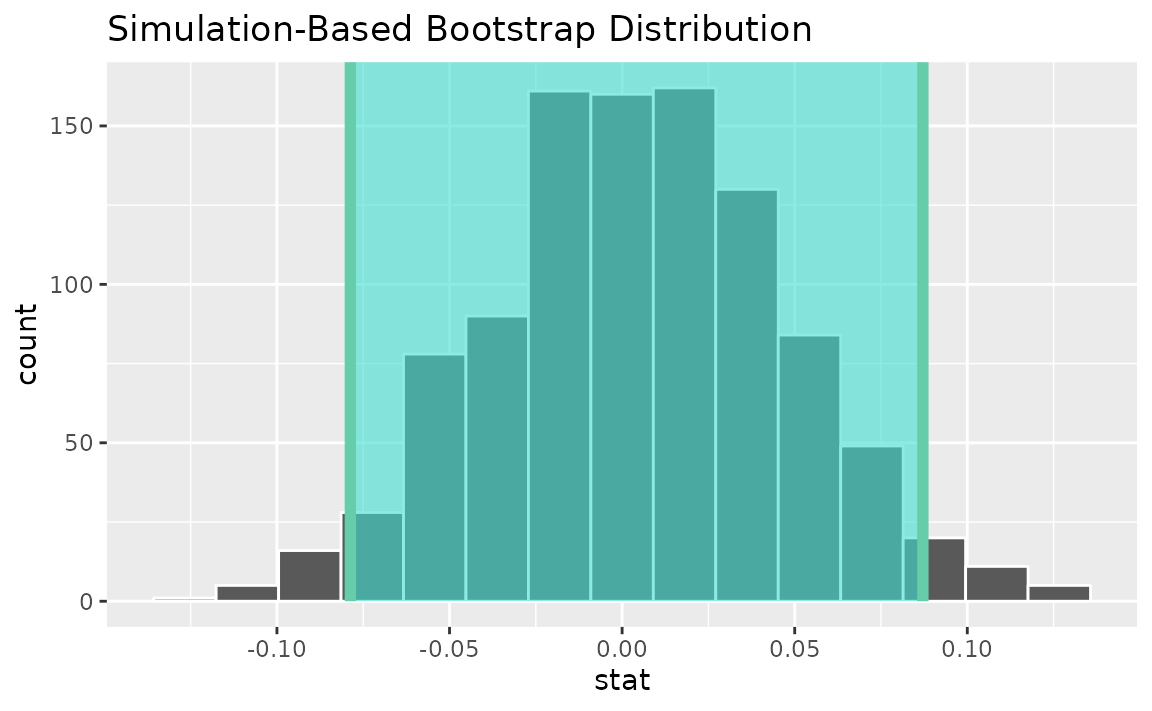

Instead of a simulation-based bootstrap distribution, we can also define a theory-based sampling distribution,

sampling_dist <- gss %>% 
  specify(college ~ sex, success = "degree") %>%
   assume(distribution = "z")

Visualization and calculation of confidence intervals interfaces in the same way as with the simulation-based distribution,

theor_ci <- get_ci(sampling_dist, point_estimate = d_hat)

theor_ci

## # A tibble: 1 × 2
##   lower_ci upper_ci
##      <dbl>    <dbl>
## 1  -0.0794   0.0878

visualize(sampling_dist) +
  shade_confidence_interval(endpoints = theor_ci)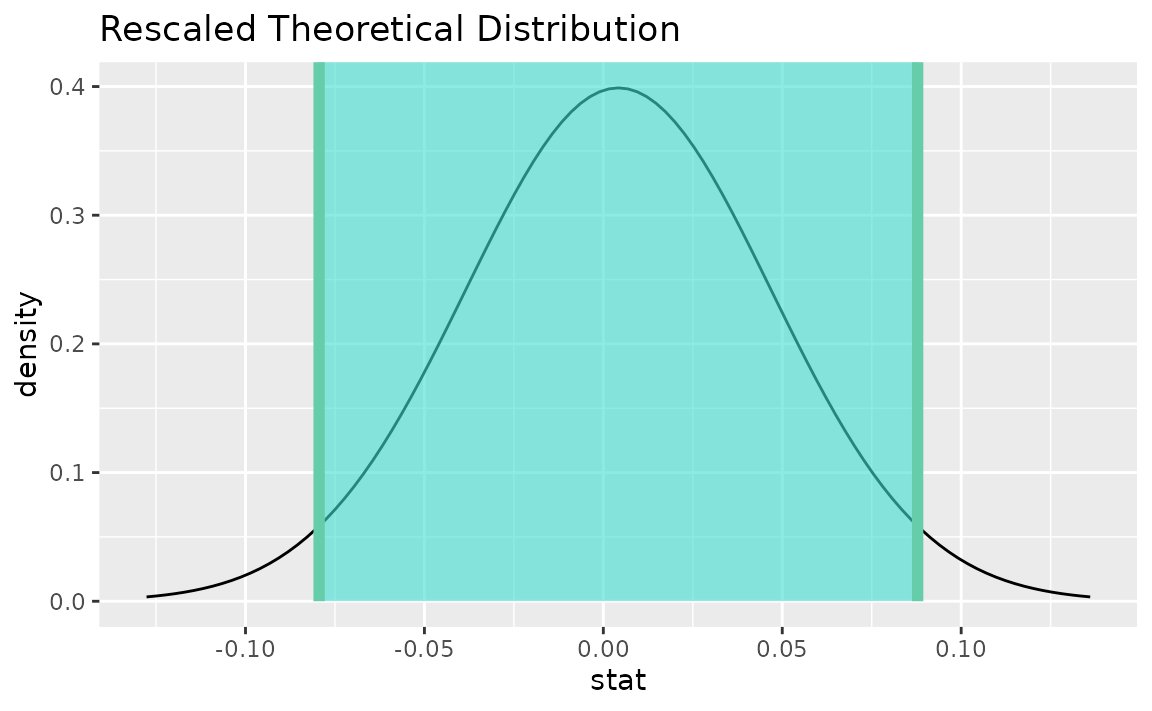

Note that the z distribution is recentered and rescaled to lie on the scale of the observed data.

Two categorical variables (z)

Finding the standardized point estimate,

z_hat <- gss %>% 
  specify(college ~ sex, success = "degree") %>%
  calculate(stat = "z", order = c("female", "male"))

Alternatively, using the observe() wrapper to calculate the observed statistic,

z_hat <- gss %>% 
  observe(college ~ sex, success = "degree",
          stat = "z", order = c("female", "male"))

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
  specify(college ~ sex, success = "degree") %>%
  generate(reps = 1000, type = "bootstrap") %>% 
  calculate(stat = "z", order = c("female", "male"))

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)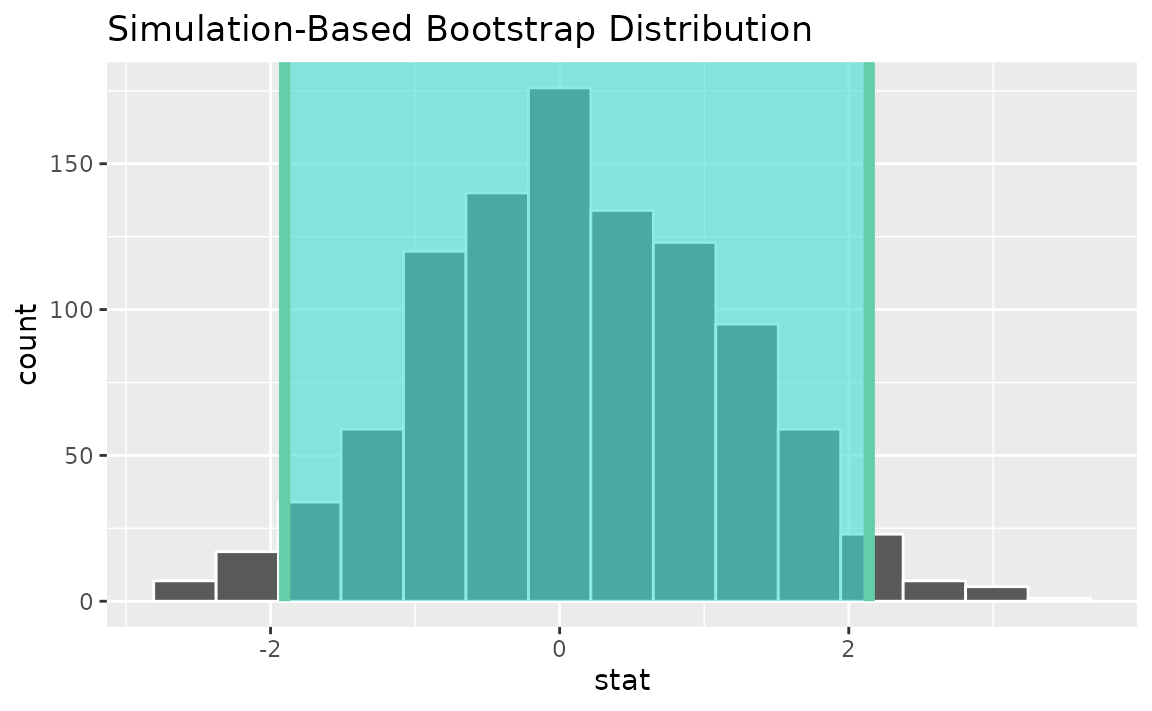

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = z_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)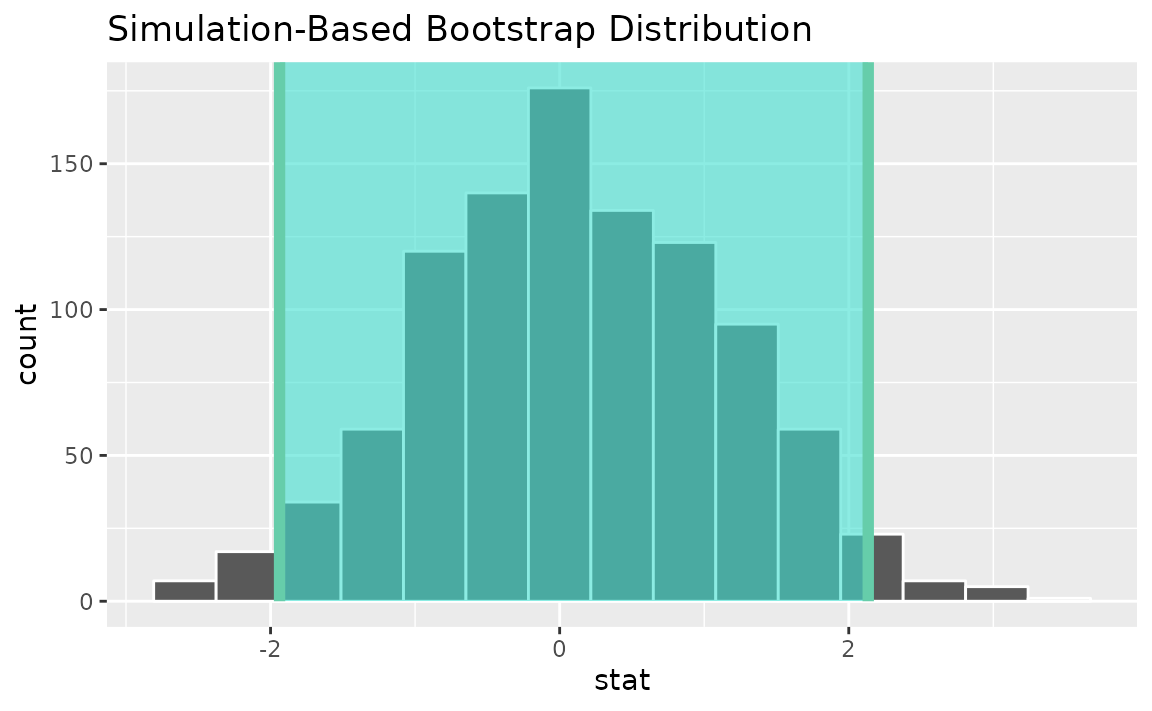

See the above subsection (diff in props) for a theory-based approach.

Two numerical vars - SLR

Finding the observed statistic,

slope_hat <- gss %>% 
  specify(hours ~ age) %>%
  calculate(stat = "slope")

Alternatively, using the observe() wrapper to calculate the observed statistic,

slope_hat <- gss %>% 
  observe(hours ~ age, stat = "slope")

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
   specify(hours ~ age) %>% 
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "slope")

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)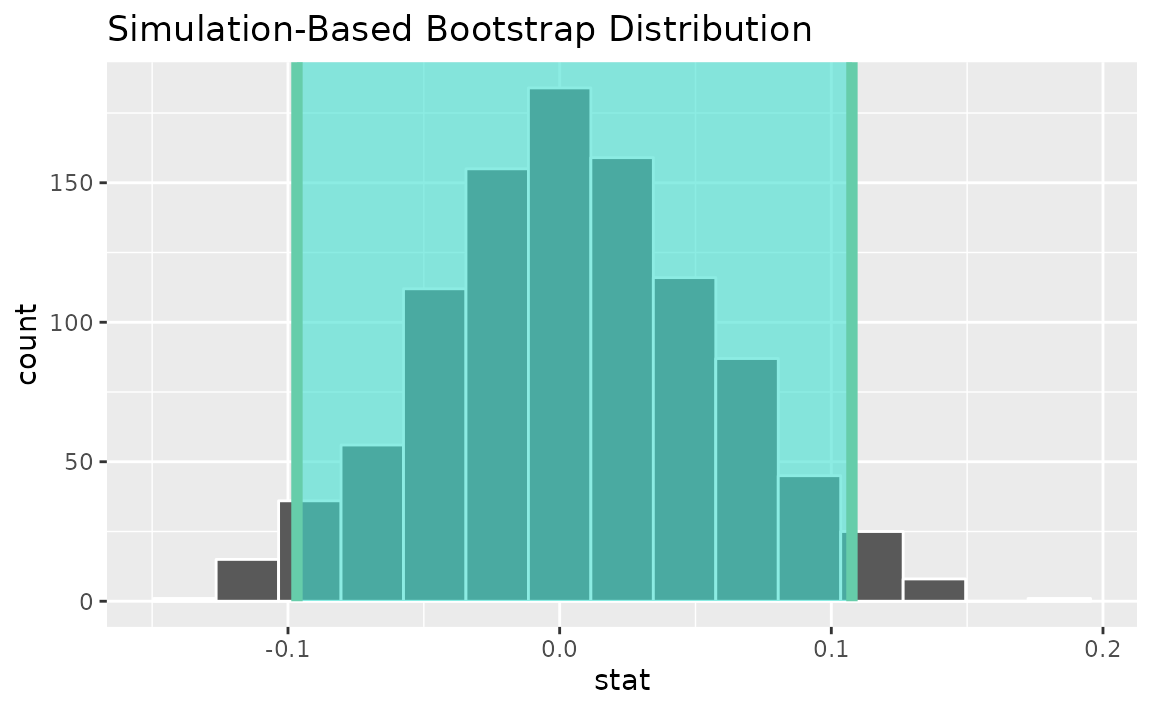

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = slope_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)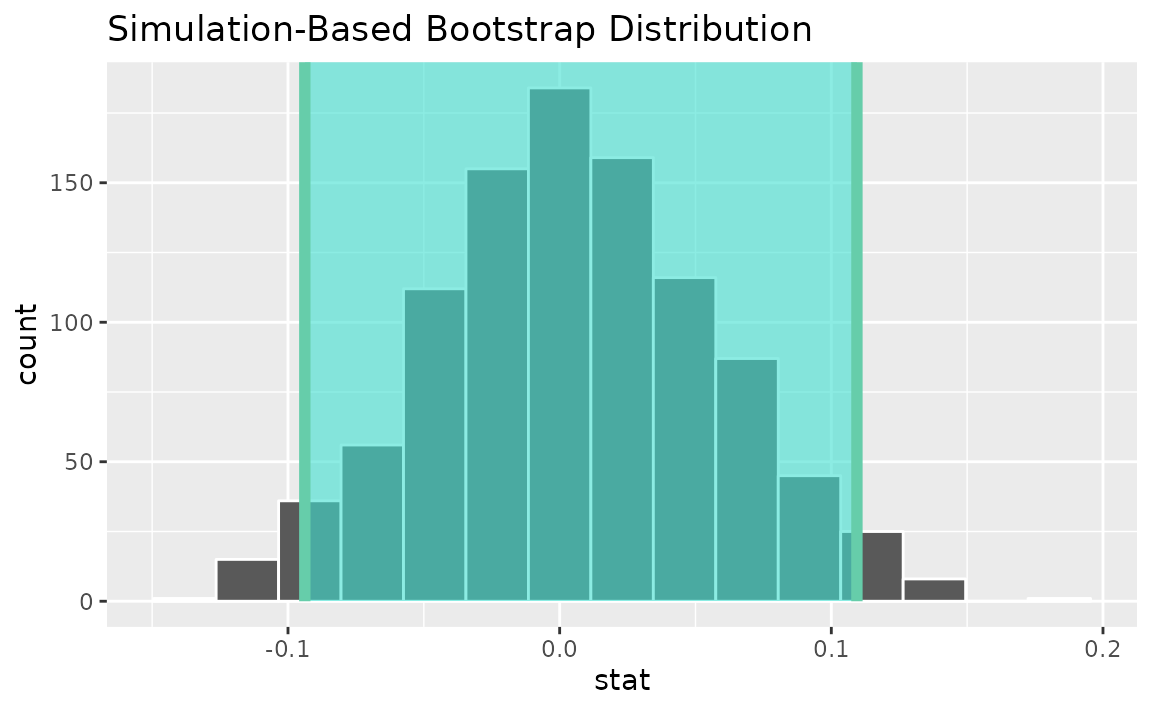

Two numerical vars - correlation

Finding the observed statistic,

correlation_hat <- gss %>% 
  specify(hours ~ age) %>%
  calculate(stat = "correlation")

Alternatively, using the observe() wrapper to calculate the observed statistic,

correlation_hat <- gss %>% 
  observe(hours ~ age, stat = "correlation")

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
   specify(hours ~ age) %>% 
   generate(reps = 1000, type = "bootstrap") %>%
   calculate(stat = "correlation")

Use the bootstrap distribution to find a confidence interval,

percentile_ci <- get_ci(boot_dist)

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci)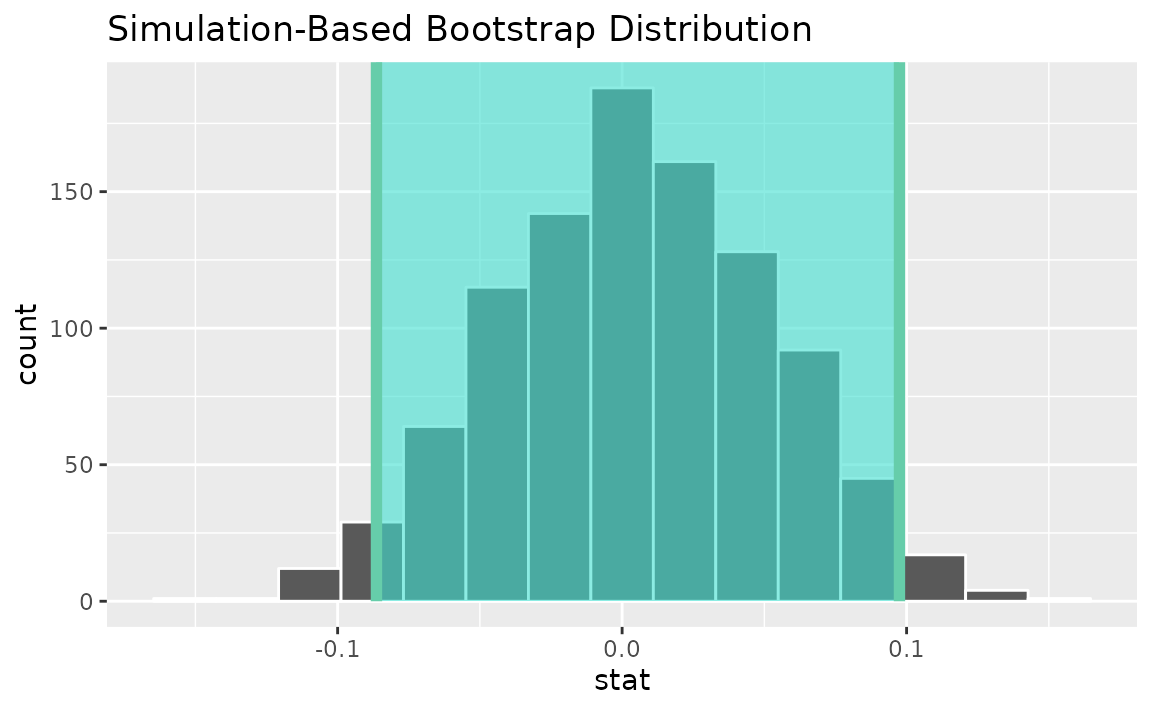

Alternatively, use the bootstrap distribution to find a confidence interval using the standard error,

standard_error_ci <- boot_dist %>%
  get_ci(type = "se", point_estimate = correlation_hat)

visualize(boot_dist) +
  shade_confidence_interval(endpoints = standard_error_ci)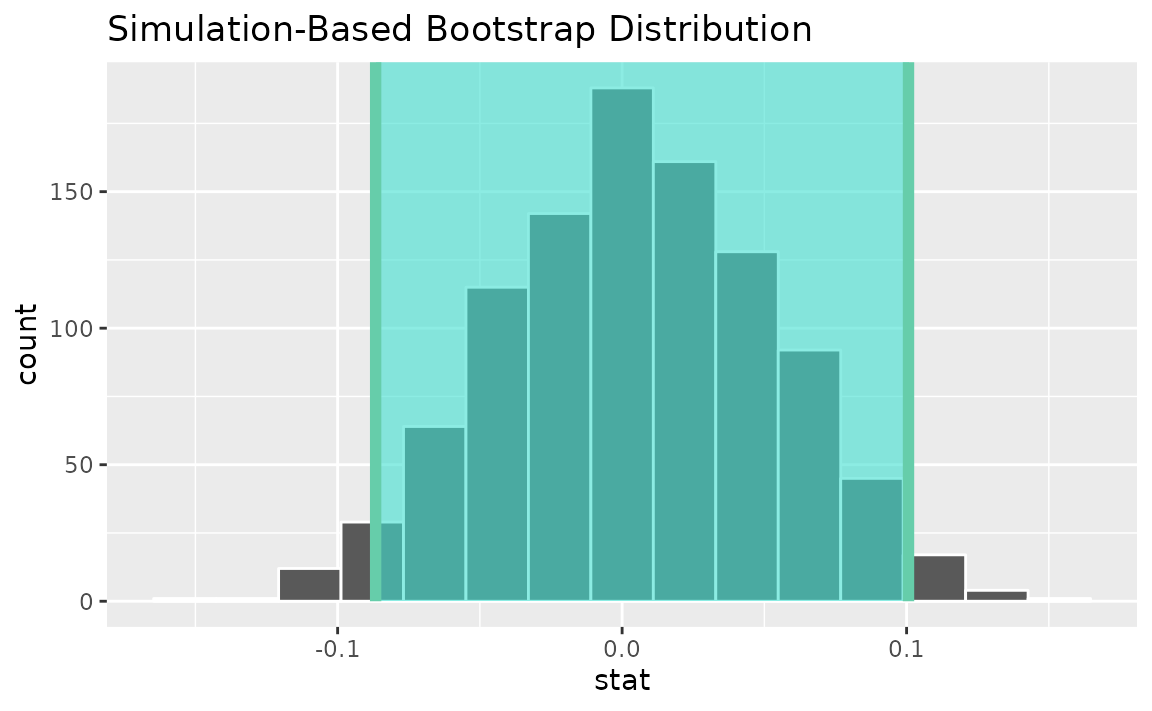

Two numerical vars - t

Not currently implemented since \(t\) could refer to standardized slope or standardized correlation.

Multiple explanatory variables

Calculating the observed fit,

obs_fit <- gss %>%
  specify(hours ~ age + college) %>%
  fit()

Then, generating a bootstrap distribution,

boot_dist <- gss %>%
  specify(hours ~ age + college) %>%
  generate(reps = 1000, type = "bootstrap") %>%
  fit()

Use the bootstrap distribution to find a confidence interval,

conf_ints <- 
  get_confidence_interval(
    boot_dist, 
    level = .95, 
    point_estimate = obs_fit
  )

Visualizing the observed statistic alongside the distribution,

visualize(boot_dist) +
  shade_confidence_interval(endpoints = conf_ints)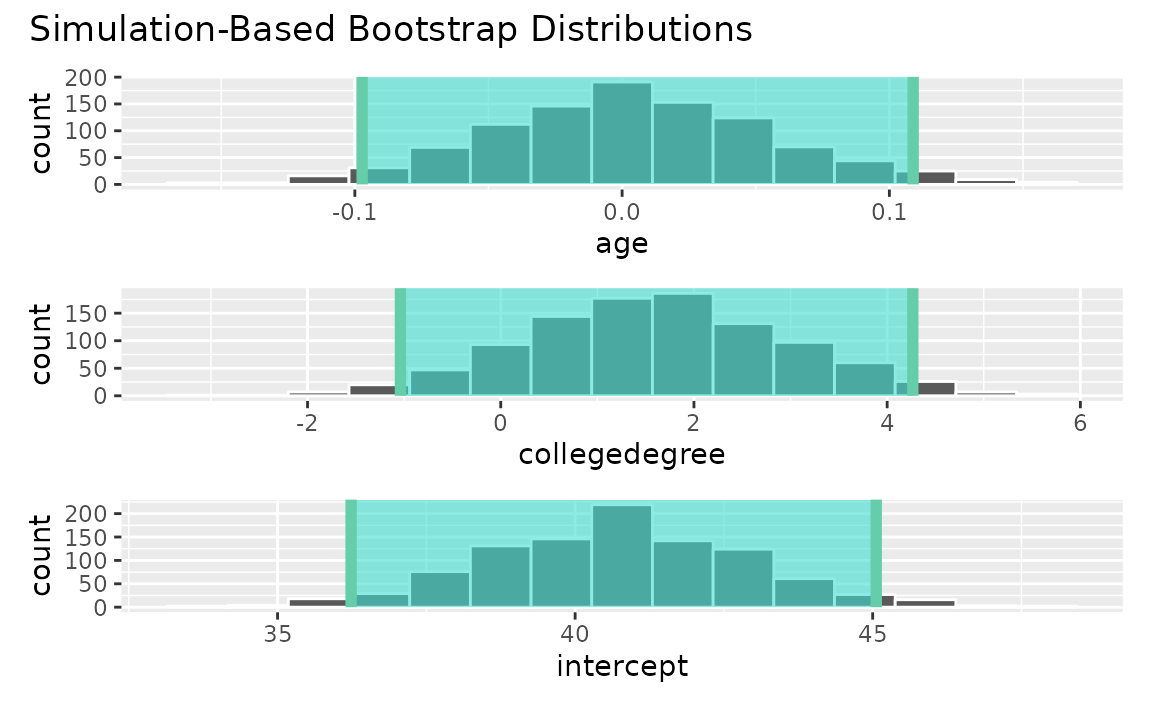

Note that this fit()-based workflow can be applied to use cases with differing numbers of explanatory variables and explanatory variable types.